早教吧作业答案频道 -->数学-->
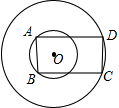
如图,两同心圆的半径分别为6、10,矩形ABCD的边AB、CD分别为两圆的弦.当矩形面积取最大值时,其周长为.
题目详情
如图,两同心圆的半径分别为6、10,矩形ABCD的边AB、CD分别为两圆的弦.当矩形面积取最大值时,其周长为___.

▼优质解答
答案和解析
连接OA,OD,作OP⊥AB于P,OM⊥AD于M,ON⊥CD于N,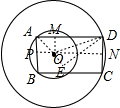
过D作DE⊥OA于E,
∵矩形APND的面积是AD×OM,△AOD的面积=
AD×OM,矩形BCNP的面积是OM×BC,
∴矩形的面积是三角形AOD的面积的4倍,
在Rt△DEO中,DE=OD×sin∠DOE=OD×sin∠AOD,
∵OA,OD的长是定值,S△AOD=
×OA×OD×sin∠AOD,
∴要使矩形ABCD的面积最大,必须△AOD的面积最大,
即当∠AOD的正弦值最大时,三角形AOD的面积最大,
∵当∠AOD≤90°时,正弦值随角度的增大而增大,
即当∠AOD=90°,S△AOD最大,
则勾股定理得:AD=
=2
,
根据三角形的面积公式求得OM=
,即AB=
.则矩形ABCD的周长是2(2
+
)=
,
故答案为:
.

过D作DE⊥OA于E,
∵矩形APND的面积是AD×OM,△AOD的面积=
| 1 |
| 2 |
∴矩形的面积是三角形AOD的面积的4倍,
在Rt△DEO中,DE=OD×sin∠DOE=OD×sin∠AOD,
∵OA,OD的长是定值,S△AOD=
| 1 |
| 2 |
∴要使矩形ABCD的面积最大,必须△AOD的面积最大,
即当∠AOD的正弦值最大时,三角形AOD的面积最大,
∵当∠AOD≤90°时,正弦值随角度的增大而增大,
即当∠AOD=90°,S△AOD最大,
则勾股定理得:AD=
| 62+102 |
| 34 |
根据三角形的面积公式求得OM=
15
| ||
| 17 |
30
| ||
| 17 |
| 34 |
30
| ||
| 17 |
128
| ||
| 17 |
故答案为:
128
| ||
| 17 |
看了 如图,两同心圆的半径分别为6...的网友还看了以下:
如图,用半径为R的圆铁皮,剪一个圆心角为α的扇形,制成一个圆锥形的漏斗,问圆心角α取什么值时,漏斗 2020-04-11 …
妈妈为小韵准备早餐,共煮了八个汤圆,其中2个是豆沙馅心,4个是果仁馅心,剩下2个是芝麻馅心,八个汤 2020-05-17 …
英语翻译三年卫盉隹三年三月既生霸壬寅,王爯旗于丰,矩白庶人取堇章于裘卫,才八十朋,厥宾,其舍田十田 2020-07-04 …
给出下列3个命题:①棱台的侧棱所在的直线必交于一点,圆台的母线所在的直线也交于一点;②一个半圆绕其 2020-07-25 …
已知正方形A、矩形B、圆C的面积为62平方厘米,其中矩形B的长是宽的2倍,如果圆周率取3.14,试 2020-07-27 …
已知圆O是边长为2的内切圆,MN为圆O的任意一条直径,点P是正方形边上的动点,则向量PM和向量PN 2020-08-01 …
以点(point)为基类,派生矩形类,与圆类,在派生类编写求面积周长的方法,分别求圆,矩形的周长与 2020-08-01 …
有一块厚度为h、半径为R的圆饼状玻璃砖,折射率为2,现经过圆心截取四分之一,如图所示.两个截面为互相 2020-11-01 …
用铁丝弯成一个上面是圆,下面是矩形的圆形,其面积为a,为使所用材料最省,底宽为多少?如题,我是这么写 2020-11-20 …
高等函数求解隧道的截面是矩形加上半圆(矩形的上底边与半圆的直径重合),其周长是15米,问矩形的底为多 2020-11-24 …