早教吧作业答案频道 -->数学-->
已知:正方形ABCD内一点E,连接EA、EB、EC.(1)若EA2+EC2=2EB2,请说明点E必在对角线AC上.(2)若EA+EB+EC的最小值为2(3+1),求正方形ABCD的边长.
题目详情
已知:正方形ABCD内一点E,连接EA、EB、EC.
(1)若EA2+EC2=2EB2,请说明点E必在对角线AC上.
(2)若EA+EB+EC的最小值为
(
+1),求正方形ABCD的边长.
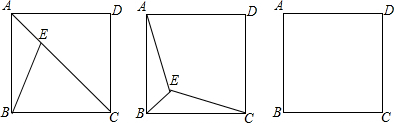
(1)若EA2+EC2=2EB2,请说明点E必在对角线AC上.
(2)若EA+EB+EC的最小值为
| 2 |
| 3 |

▼优质解答
答案和解析
(1)证明:如图1中,将△ABE绕点B顺时针旋转90°得△CBE′,连接EE′.
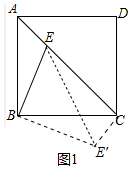
∵BE=BE′,∠EBE′=90°,AE=CE′,
∴EE′=
BE,
∵EA2+EC2=2EB2,
∴CE′2+EC2=EE′2,
∴∠ECE′=90°,
∴∠ECB+∠BCE′=∠ECB+∠BAE=90°,
∴A、E、C共线,
∴点E在正方形ABCD的对角线上.
(2) 如图2中,将△ABE绕点B逆时针旋转60°得△A′BE′,连结A′C,作A′H⊥BC于H.
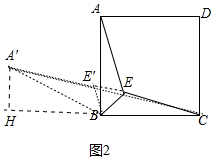
∵△ABE绕点B逆时针旋转60°得△A′BE′,
∴BE=BE′,∠EBE′=60°,
∴△EBE′为等边三角形,
∴EE′=BE,
∴A′E′=AE,BA′=BA=2,∠ABA′=60°,
∵A′E′+E′E+EC≥A′C,
∴AE+BE+CE≥AC(当且仅当点E′、点E在AC上时,取等号),
∴AE+BE+CE有最小值,最小值为A′C的长,设正方形的边长为a,
在Rt△A′BH中,∠A′BH=30°,
∴A′H=
A′B=
a,BH=
A′H=
a,
∴CH=a+
a,
在Rt△A′CH中,A′C2=A′H2+CH2,
∴(
a)2+(a+
a)2=(
+
)2,
解得a=2.
∴正方形的边长为2.

∵BE=BE′,∠EBE′=90°,AE=CE′,
∴EE′=
| 2 |
∵EA2+EC2=2EB2,
∴CE′2+EC2=EE′2,
∴∠ECE′=90°,
∴∠ECB+∠BCE′=∠ECB+∠BAE=90°,
∴A、E、C共线,
∴点E在正方形ABCD的对角线上.
(2) 如图2中,将△ABE绕点B逆时针旋转60°得△A′BE′,连结A′C,作A′H⊥BC于H.

∵△ABE绕点B逆时针旋转60°得△A′BE′,
∴BE=BE′,∠EBE′=60°,
∴△EBE′为等边三角形,
∴EE′=BE,
∴A′E′=AE,BA′=BA=2,∠ABA′=60°,
∵A′E′+E′E+EC≥A′C,
∴AE+BE+CE≥AC(当且仅当点E′、点E在AC上时,取等号),
∴AE+BE+CE有最小值,最小值为A′C的长,设正方形的边长为a,
在Rt△A′BH中,∠A′BH=30°,
∴A′H=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| ||
| 2 |
∴CH=a+
| ||
| 2 |
在Rt△A′CH中,A′C2=A′H2+CH2,
∴(
| 1 |
| 2 |
| ||
| 2 |
| 6 |
| 2 |
解得a=2.
∴正方形的边长为2.
看了 已知:正方形ABCD内一点E...的网友还看了以下:
有黑色固体a和白色固体b,分别与盐酸反应都有相同气体c生成,同时,分别生成产物d和eb的水溶液中滴 2020-04-25 …
热学ΔE,ΔH,q,w,ΔU,ΔE,ΔH,q,w,ΔU,怎么好像ΔE,ΔU都是内能的意思.有什么区 2020-04-27 …
初二相似问题在梯形ABCD中,AD‖BC,E、F分别为AB,CD上一点,且梯形AEFD∽梯形EBC 2020-05-01 …
按照生物体结构层次的从小到大排列,正确的图形排序是()A.A→B→C→D→EB.C→E→A→D→B 2020-05-02 …
按照生物体结构层次的从小到大排列,正确的图形排序是()A、A→B→C→D→EB、C→E→A→D→B 2020-05-02 …
一直p为曲线c上任一点,若p到点F(1/2,0)的距离与p带直线x=-1/2距离相等求曲线方程试问 2020-05-14 …
(2009•本溪二模)如图,⊙O上两点C、E关于直径AB对称,连接AC、BC,过C作CE的垂线,交 2020-05-14 …
梯形ABCD中,AD平行于BC,E.F分别是AB和CD边上的点,且梯形AEFD相似于梯形EBCF, 2020-05-15 …
在意外伤害保险中,判断是否构成伤害,要求( )。A.致害物必须是外来的B.致害物必须是内部的C.致害 2020-05-22 …
已知三角形ABC,AC=BC,角C=90度,在直角三角形ADE中,AD=DE,点M是EB的中点.如 2020-05-23 …