早教吧作业答案频道 -->数学-->
已知直三棱柱ABC-A1B1C1中,上底面是斜边为AC的直角三角形,E、F分别是A1B、AC1的中点.(1)求证:EF∥平面ABC;(2)求证:平面AEF⊥平面AA1B1B.
题目详情
已知直三棱柱ABC-A1B1C1中,上底面是斜边为AC的直角三角形,E、F分别是A1B、AC1的中点.
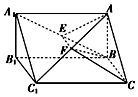
(1)求证:EF∥平面ABC;
(2)求证:平面AEF⊥平面AA1B1B.

(1)求证:EF∥平面ABC;
(2)求证:平面AEF⊥平面AA1B1B.
▼优质解答
答案和解析
证明:(1)连接A1C,直三棱柱ABC-A1B1C1中,四边形AA1C1C是矩形,
所以点F在A1C上,且F为A1C的中点,
在△A1BC中,E、F分别是A1B、AC1的中点,
所以EF∥BC;
又EF⊄平面ABC,BC⊂平面ABC,
所以EF∥平面ABC;
(2)在直三棱柱ABC-A1B1C1中,BB1⊥平面ABC,
所以BB1⊥BC,
因为EF∥BC,
所以BB1⊥EF;
又底面是斜边为AC的直角三角形,故AB⊥BC,
所以EF⊥AB,
又BB1∩AB=B,
所以EF⊥平面AA1B1B,
又EF⊂平面AEF,
所以平面AEF⊥平面AA1B1B.
所以点F在A1C上,且F为A1C的中点,
在△A1BC中,E、F分别是A1B、AC1的中点,
所以EF∥BC;
又EF⊄平面ABC,BC⊂平面ABC,
所以EF∥平面ABC;
(2)在直三棱柱ABC-A1B1C1中,BB1⊥平面ABC,
所以BB1⊥BC,
因为EF∥BC,
所以BB1⊥EF;
又底面是斜边为AC的直角三角形,故AB⊥BC,
所以EF⊥AB,
又BB1∩AB=B,
所以EF⊥平面AA1B1B,
又EF⊂平面AEF,
所以平面AEF⊥平面AA1B1B.
看了 已知直三棱柱ABC-A1B1...的网友还看了以下:
下列命题正确的是()A.三角形的外心到三边距离相等B.三角形的内心不一定在三角形的内部C.等边三角 2020-05-16 …
已知:如图,△ABD和△ACE均为等边三角形,且∠DAB=∠CAE=60°,那么△ADC≌△AEB 2020-06-04 …
三角形的三条高所在的直线相交于一点,这个交点的位置在()A.三角形内B.三角形外C.三角形边上D. 2020-06-15 …
下列说法正确的是A.三角形的中线就是过顶点平分对边的直线B三角形的高就是顶点到对边的距离下列说法正 2020-07-20 …
三角形ABC的内角A,B,C的对边分别为a,b,c,已知a=bcosC+csinB.(1)求B.三 2020-07-30 …
下列说法中正确的是A.三角形的外心是三边中线的交点;B.三角形的外心一定在三角形外部;C.等腰三角 2020-07-30 …
下列说法中正确的是()A.从三角形一个顶点向它对边所在直线画垂线,此垂线段是三角形的高B.三角形的 2020-08-02 …
关于三角形,下列说法错误的是()A.三角形具有稳定性B.三角形任意两边之和大于第三边C.三角形的内 2020-08-03 …
已知三角形abc相似三角形a'b'c',对应边的中线之比为3:2,三角形a'b'c'的周长为24, 2020-08-03 …
函数题,A是不是B的函数(1)A等边三角形的面积B等边三角形的边长这两者是不是函数关系,A是不是B 2020-08-03 …