早教吧作业答案频道 -->数学-->
如图,直线BF、CG分别交直线AD、EM于点B、F、C、G.BN、FN分别平分∠ABF、∠BFE,且∠ABN与∠EFN互为余角.(1)判断直线AD与直线EM的位置关系,并说明理由;(2)若图中∠1=∠2,判断∠P,∠Q
题目详情
如图,直线BF、CG分别交直线AD、EM于点B、F、C、G.BN、FN分别平分∠ABF、∠BFE,且∠ABN与∠EFN互为余角.
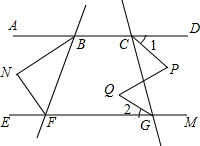
(1)判断直线AD与直线EM的位置关系,并说明理由;
(2)若图中∠1=∠2,判断∠P,∠Q的大小关系,并说明理由.

(1)判断直线AD与直线EM的位置关系,并说明理由;
(2)若图中∠1=∠2,判断∠P,∠Q的大小关系,并说明理由.
▼优质解答
答案和解析
(1)AD∥EM,
∵BN、FN分别平分∠ABF、∠BFE,
∴∠ABN=
∠ABF,∠EFN=
∠EFB,
∵∠ABN与∠EFN互为余角,
∴∠ABF与∠EFB互补,
∴AD∥EM;
(2)∠P=∠Q,
∵AD∥EM,
∴∠DCG=∠CGF,
∵∠1=∠2,∠1+∠PCG=∠DCG,∠2+∠CGQ=∠CGF
∴∠PCG=∠CGQ,
∴CP∥QG,
∴∠P=∠Q.
∵BN、FN分别平分∠ABF、∠BFE,
∴∠ABN=
| 1 |
| 2 |
| 1 |
| 2 |
∵∠ABN与∠EFN互为余角,
∴∠ABF与∠EFB互补,
∴AD∥EM;
(2)∠P=∠Q,
∵AD∥EM,
∴∠DCG=∠CGF,
∵∠1=∠2,∠1+∠PCG=∠DCG,∠2+∠CGQ=∠CGF
∴∠PCG=∠CGQ,
∴CP∥QG,
∴∠P=∠Q.
看了 如图,直线BF、CG分别交直...的网友还看了以下:
● 路由器的S0 端口连接(13) 。 (13)A. 广域网 B. 以太网 C. 集线器 D. 交换 2020-05-26 …
路由器的S0端口连接____.A.广域网B.以太网C.集线器D.交换机 2020-05-26 …
数学问题.希望解题思路清晰!因做不来图!只能用文字叙述!希望能不用勾股定理来解答!1.三角形ABC 2020-06-10 …
抛物线y=x^2-2x-3与x轴交与A,B两点,与y轴交与C点.设直线y=-x+3与y轴的交点抛物 2020-06-14 …
在△ABC中,E是AC中点,过E的直线交BC延长线于D,交AB于F,且AF=2,BF=4,BD=5 2020-07-12 …
已知三角形ABC顶点A的直线交BC的延长线于D,交三角形ABC的外接圆于点F若AB是三角形ABC的 2020-07-14 …
一个三角形ABC,角A为60度,角B角C的角平分线分别交AB于D交AC于E两线交于点F连接D,E有 2020-07-30 …
在三角形ABC中,角A角B的平分线分别交对边于D,E角C的外角平分线交对边延长线于F,求证:D、E 2020-08-03 …
在三角形abc中角bac=90°ab=ac,角abc的平分线交ac于d,过垂线bd垂线交bdd的延长 2020-12-25 …
如图,Rt△ABC中,∠CBA=90°,∠CAB的角平分线AP和∠ACB的外角平分线CF相交于点D, 2021-01-02 …