如图所示，在矩形ABCD中，对角线AC，BD相交于点O．过点O作OE⊥BC于点E，连接DE交OC于点F，过点F作FG⊥BC于点G，则△ABC与△FGC是位似图形吗？若是，请说出位似中心，并求出相似比；若不是，

Question

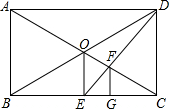
如图所示，在矩形ABCD中，对角线AC，BD相交于点O．过点O作OE⊥BC于点E，连接DE交OC于点F，过点F作FG⊥BC于点G，则△ABC与△FGC是位似图形吗？若是，请说出位似中心，并求出相似比；若不是，请说明理由．

Answer 1

△ABC与△FGC是位似图形，
∵OE⊥BC，FG⊥BC，
∴OE∥FG，又OF、EG的连线相交于点C，
∴△ABC与△FGC是位似图形，位似中心是点C，
∵四边形ABCD是矩形，
∴∠BCD=90°，OB=OD，又OE⊥BC，
∴OE∥CD，
∴OE是△BCD的中位线，
∴OE=(1)/(2)CD，
∵OE∥CD，
∴(OF)/(FC)=(OE)/(CD)=(1)/(2)，则(CF)/(CO)=(2)/(3)，
∴△ABC与△FGC的相似比是3．