早教吧作业答案频道 -->数学-->
如图1,△ABC为等边三角形,△ADE是△ABC的位似图形,位似比为k:1,点D在AB上,点E在AC上,点E在AC上.(1)证明:DE∥BC.(2)将△ADE绕点A旋转α至△AMN的位置,如图2,当AM⊥BC时,请你判
题目详情
如图1,△ABC为等边三角形,△ADE是△ABC的位似图形,位似比为k:1,点D在AB上,点E在AC上,点E在AC上.
(1)证明:DE∥BC.
(2)将△ADE绕点A旋转α至△AMN的位置,如图2,当AM⊥BC时,请你判断AC与MN的位置关系,并说明理由.
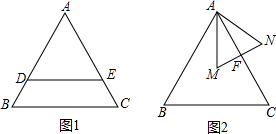
(1)证明:DE∥BC.
(2)将△ADE绕点A旋转α至△AMN的位置,如图2,当AM⊥BC时,请你判断AC与MN的位置关系,并说明理由.

▼优质解答
答案和解析
(1)证明:∵△ADE是△ABC的位似图形,
∴△ADE∽△ABC,
∴∠ADE=∠B,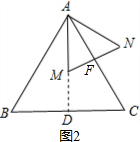
∴DE∥BC;
(2)AC⊥MN.
证明:如图2,延长AM交BC于D,
∵△ABC是等边三角形,
∴AB=AC,∠BAC=60°,
∴∠DAC=30°,又∠AMN=60°,
∴∠AFM=90°,即AC⊥MN.
∴△ADE∽△ABC,
∴∠ADE=∠B,

∴DE∥BC;
(2)AC⊥MN.
证明:如图2,延长AM交BC于D,
∵△ABC是等边三角形,
∴AB=AC,∠BAC=60°,
∴∠DAC=30°,又∠AMN=60°,
∴∠AFM=90°,即AC⊥MN.
看了 如图1,△ABC为等边三角形...的网友还看了以下:
已知二次函数y=x*x+4x与x轴交于B,O两点,顶点为A,连接AB,过原点O作AB的平行线得到直 2020-04-27 …
动中有静,静中有动,这种观点是?()A:形而上学B:唯实论C:诡辩论D:辨证论为什么他们的不同之处 2020-05-16 …
乳癖的肿块特点是( )A.形如鸡卵,光滑,柔韧,活动,无痛B.坚硬如石,表面不平,固定不 2020-05-17 …
如图,坐标原点O为矩形ABCD的对称中心,顶点A的坐标为(1,t),AB∥x轴,矩形A′B′C′D 2020-06-14 …
如图,正方形ABCD的对角线AC、BD相交于点O,正方形A′B′C′D′的顶点A′与点O重合,A′ 2020-06-15 …
已知三角形ABC的三个顶点,A(1,3)B(-4,1)C(2,-1)1.若三角形ABC中任意一点P 2020-08-02 …
如图,多边形的各顶点都在方格纸的格点(横竖格子线的交错点)上,这样的多边形称为格点多边形,它的面积S 2020-11-01 …
大一常微分方程A,B,C,D四个动点开始时分别位于一个正方形的四个顶点,然后A点向着B点,B点向着C 2020-12-15 …
三角形ABC和A'BC存在某种对应关系(关于BC对称),其中A(3,6)对应点是A'(3,0)三角形 2020-12-17 …
在平面直角坐标系中,O为原点,四边形ABCD为矩形,点A,C坐标分别为急,有悬赏!在平面直角坐标系中 2020-12-25 …