早教吧作业答案频道 -->数学-->
如图,D、E分别是不等边三角形ABC(即AB≠BC≠AC)的边AB、AC的中点,点O是在△ABC的内部的一个动点,连接OA、OB、OC,点G、F分别是OB、OC的中点,顺次连接点D、G、F、E.(1)求证:四边形DEF
题目详情
如图,D、E分别是不等边三角形ABC(即AB≠BC≠AC)的边AB、AC的中点,点O是在△ABC的内部的一个动点,连接OA、OB、OC,点G、F分别是OB、OC的中点,顺次连接点D、G、F、E.
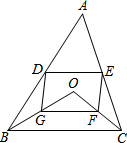
(1)求证:四边形DEFG是平行四边形;
(2)当OA=BC时,求证:四边形DEFG是菱形.

(1)求证:四边形DEFG是平行四边形;
(2)当OA=BC时,求证:四边形DEFG是菱形.
▼优质解答
答案和解析
 (1)证明:∵D、E分别是边AB、AC的中点.
(1)证明:∵D、E分别是边AB、AC的中点.
∴DE∥BC,DE=
BC.
同理,GF∥BC,GF=
BC.
∴DE∥GF,DE=GF.
∴四边形DEFG是平行四边形.
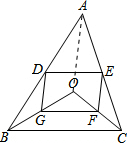
(2)证明:如图,连接OA.由(1)得出四边形DEFG是平行四边形,
∵AO=BC,
∴GD=
AO,GF=
BC,
∴DG=GE,
∴平行四边形DEFG是菱形.
 (1)证明:∵D、E分别是边AB、AC的中点.
(1)证明:∵D、E分别是边AB、AC的中点.∴DE∥BC,DE=
| 1 |
| 2 |
同理,GF∥BC,GF=
| 1 |
| 2 |
∴DE∥GF,DE=GF.
∴四边形DEFG是平行四边形.
(2)证明:如图,连接OA.由(1)得出四边形DEFG是平行四边形,
∵AO=BC,
∴GD=
| 1 |
| 2 |
| 1 |
| 2 |
∴DG=GE,
∴平行四边形DEFG是菱形.
看了 如图,D、E分别是不等边三角...的网友还看了以下:
在三棱锥O——ABC中,三条棱OA,OB,OC两两垂直,且OA=OB=OC,M是AB边的中点,则O 2020-04-12 …
如图,大圆O的半径为6cm,弦AB=6cm,OC⊥AB于点C,以O为圆心,OC为半径作圆交OA,O 2020-04-27 …
(2011•广州一模)如图,在△ABC中,AB=5,BC=3,∠ABC=120°,D是AB上一点, 2020-05-13 …
△ABC是一个等边三角形,O是△ABC的三边的垂直平分线的交点,AB=AC=BC=a,AO=OB= 2020-05-22 …
半圆O的直径AB=12,半径OC⊥AB,⊙O‘与半圆O相内切,并且与OB,OC相切于点D,F.求⊙ 2020-06-06 …
已知三棱锥O-ABC中,它的底面边长和侧棱长除OC外都是3,并且侧面0AB与底面ABC所成的角是6 2020-06-11 …
(2013•常州)在平面直角坐标系xOy中,已知点A(6,0),点B(0,6),动点C在以半径为3 2020-06-14 …
在梯形ABCO中,OC∥AB,以O为原点建立平面直角坐标系,A、B、C三点的坐标分别是A(8,0) 2020-06-14 …
(2013•白下区二模)D、E分别是不等边三角形ABC(即AB≠BC≠AC)的边AB、AC的中点. 2020-06-15 …
某同学为体验所学知识,做了如图所示的实验.他让铅笔保持水平,铅笔尖B顶在手心,手掌保持竖直,用细线 2020-06-22 …