早教吧作业答案频道 -->数学-->
如图,在平面直角坐标系xOy中,点A,B在双曲线y=kx(k是常数,且k≠0)上,过点A作AD⊥x轴于点D,过点B作BC⊥y轴于点C,已知点A的坐标为(4,32),四
题目详情
如图,在平面直角坐标系xOy中,点A,B在双曲线y=
(k是常数,且k≠0)上,过点A作AD⊥x轴于点D,过点B作BC⊥y轴于点C,已知点A的坐标为(4,
),四边形ABCD的面积为4,则点B的坐标为___.
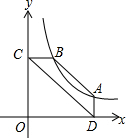
| k |
| x |
| 3 |
| 2 |

▼优质解答
答案和解析
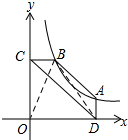 连接BO、BD,
连接BO、BD,
∵点A在双曲线y=
(k是常数,且k≠0)上,点A的坐标为(4,
),
∴k=4×
=6,
又∵BC⊥y轴于点C,
∴BC∥OD,
∴△BOC的面积=△BCD的面积=3,
又∵四边形ABCD的面积为4,
∴△ABD的面积=4-3=1,
设B(a,
),
∵AD⊥x轴于点D,A的坐标为(4,
),
∴AD=
,
∵
×
×(4-a)=1,
解得a=
,
∴
=
,
∴点B的坐标为(
,
).
故答案为:(
,
).
 连接BO、BD,
连接BO、BD,∵点A在双曲线y=
| k |
| x |
| 3 |
| 2 |
∴k=4×
| 3 |
| 2 |
又∵BC⊥y轴于点C,
∴BC∥OD,
∴△BOC的面积=△BCD的面积=3,
又∵四边形ABCD的面积为4,
∴△ABD的面积=4-3=1,
设B(a,
| 6 |
| a |
∵AD⊥x轴于点D,A的坐标为(4,
| 3 |
| 2 |
∴AD=
| 3 |
| 2 |
∵
| 1 |
| 2 |
| 3 |
| 2 |
解得a=
| 8 |
| 3 |
∴
| 6 |
| a |
| 9 |
| 4 |
∴点B的坐标为(
| 8 |
| 3 |
| 9 |
| 4 |
故答案为:(
| 8 |
| 3 |
| 9 |
| 4 |
看了 如图,在平面直角坐标系xOy...的网友还看了以下:
如图点D在反比例函数y=k/x(k>0)的图像上,点C在x轴的正半轴上且坐标为(4,O),△ODC 2020-05-17 …
在平面直角坐标系中,矩形OABC,O(0,0),A(2,0),C(0,1),将矩形折叠,使O点落在 2020-05-20 …
通达信阳包阴k线(五彩k线)公式求改为主图相应k线上加特殊图标形式通达信阳包阴k线(五彩k线)公式 2020-07-23 …
如图所示,O的直径的长是关于x的二次方程x2+2(k-2)x+k=0(k是整数)的最大整数根.P是 2020-07-31 …
已知圆O的直径长为关于x的方程x^2+2(k-2)x+k=0的最大整数根(k为整数)快进来啊已知圆 2020-07-31 …
如图所示,⊙O的直径的长是关于x的二次方程x2+2(k-2)x+k=0(k是整数)的最大整数根.P 2020-07-31 …
如图,已知直线y=1/2x与双曲线y=k/x(k>0)交于A.B两点,且点A的横坐标为4,1.求K 2020-08-01 …
如图,已知直线y=1/2x与双曲线y=k/x(k>0)交于A.B两点,且点A的横坐标为4,1.求K 2020-08-01 …
一元二次方程根的分布情况,如下,1.两根都大于k:的塔>=o,-b/2a>k,f(k)>o2.两根都 2020-11-12 …
使用mathematica求解多元不等式整数解出错,tt={10.11,14.31,17.48,25 2020-12-14 …