早教吧作业答案频道 -->数学-->
如图,在平面直角坐标系中,四边形OABC是矩形,点B(10,4),D是矩形边BC上的一点,将矩形沿过点D的直线折叠,使B的对应点B′落在x轴的正半轴上(1)当点O与B′重合时,点D的坐标为
题目详情
如图,在平面直角坐标系中,四边形OABC是矩形,点B(10,4),D是矩形边BC上的一点,将矩形沿过点D的直线折叠,使B的对应点B′落在x轴的正半轴上
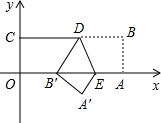
(1)当点O与B′重合时,点D的坐标为___;
(2)连接B′C′,若△B′DC是以B′D为腰的等腰三角形,则点B′的坐标是___.

(1)当点O与B′重合时,点D的坐标为___;
(2)连接B′C′,若△B′DC是以B′D为腰的等腰三角形,则点B′的坐标是___.
▼优质解答
答案和解析
(1)如图1中,当B′与O重合时,设BD=DO=x,
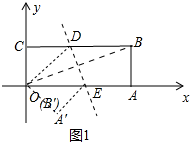
在Rt△CDO中,∵OD2=CD2+CO2,
∴x2=(10-x)2+42,
∴x=5.8,
∴CD=10-5.8=4.2,
∴点D坐标(4.2,4).
故答案为(4.2,4).
(2)如图2中,当DB′=CD=DB=5时,作DM⊥OA于M,
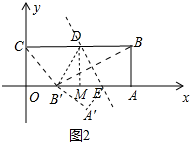
在Rt△DMB′中,MB′=
=3,
∴OB′=OM-MB′=2,
∴B′坐标为(2,0).
如图3中,当DB′=B′C时,设OB′=x,则CM=MD=x,DB=DB′=B′C=10-2x,
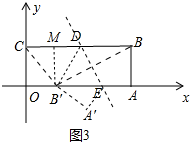
在Rt△COB′中,∵B′C2=CO2+OB′2,
∴(10-2x)2=42+x2,
∴x=
或
(舍弃),
综上所述若△B′DC是以B′D为腰的等腰三角形,则点B′的坐标为(2,0)或(
,0).
故答案为(2,0)或(
,0).

在Rt△CDO中,∵OD2=CD2+CO2,
∴x2=(10-x)2+42,
∴x=5.8,
∴CD=10-5.8=4.2,
∴点D坐标(4.2,4).
故答案为(4.2,4).
(2)如图2中,当DB′=CD=DB=5时,作DM⊥OA于M,

在Rt△DMB′中,MB′=
| DB′2-DM2 |
∴OB′=OM-MB′=2,
∴B′坐标为(2,0).
如图3中,当DB′=B′C时,设OB′=x,则CM=MD=x,DB=DB′=B′C=10-2x,

在Rt△COB′中,∵B′C2=CO2+OB′2,
∴(10-2x)2=42+x2,
∴x=
20-2
| ||
| 3 |
20+2
| ||
| 3 |
综上所述若△B′DC是以B′D为腰的等腰三角形,则点B′的坐标为(2,0)或(
20-2
| ||
| 3 |
故答案为(2,0)或(
20-2
| ||
| 3 |
看了 如图,在平面直角坐标系中,四...的网友还看了以下:
在直角坐标系中有点A(a,b),B(a,c),C(-a,-b),D(-a,-c)(a≠0,b≠c) 2020-04-27 …
学校组织春游,让同学自备午餐,A,B,C约好一起买面包,A身上的钱多,可C没钱.他们先买了九个面包 2020-05-13 …
已知实数a,b,c的大小关系如图所示: 化简|2a-b|+3(c-a)-2|b-c|数轴从左到右分 2020-05-15 …
在直角坐标系中有点A(a.b)B(a.c)C(-a.-b)D(-a.-c)(a≠0b≠c)若要使四 2020-05-19 …
{a}{a,b,c}应该填什么?{a}是{a,b,c}的真子集{a}是{a,b,c}的子集 2020-07-08 …
设l直线的方程为Ax+By+c=0(a,b不同时为0),根据下列条件,求出A,B,C应满足的条件( 2020-07-13 …
如果直线Ax+By+C=0(其中A,B,C均不为0)不通过第一象限,则A,B,C应满足条件什么?A 2020-07-30 …
(a+b)×c=a×c+b×c应用了[]A.乘法交换律B.乘法结合律C.乘法分配律 2020-07-31 …
(a+b)×c=a×c+b×c应用的是()A.加法结合律B.乘法分配律C.乘法结合律D.加法交换律 2020-07-31 …
设定数A,B,C使得不等式A(x-y)(x-z)+B(y-z)(y-x)+C(z-x)(z-y)≥ 2020-08-03 …