早教吧作业答案频道 -->数学-->
如图,△ABC与△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,分别作▱ABFD与▱ACGE,连接AF,CE.(1)当点D在△ABC外,如图1,求证:AF=CE,AF⊥CE;(2)当点D在△ABC内,如图2,问题(1)中的结论
题目详情
如图,△ABC与△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,分别作▱ABFD与▱ACGE,连接AF,CE.
(1)当点D在△ABC外,如图1,求证:AF=CE,AF⊥CE;
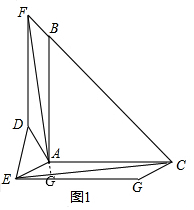
(2)当点D在△ABC内,如图2,问题(1)中的结论是否成立?若成立,给出证明;若不成立,说明理由.
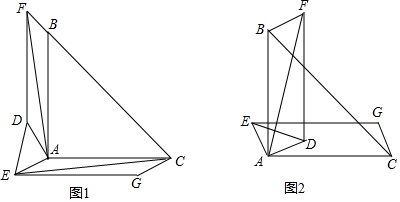
(1)当点D在△ABC外,如图1,求证:AF=CE,AF⊥CE;
(2)当点D在△ABC内,如图2,问题(1)中的结论是否成立?若成立,给出证明;若不成立,说明理由.

▼优质解答
答案和解析
 证明:(1)如图1,∵△ABC与△ADE都是等腰直角三角形,
证明:(1)如图1,∵△ABC与△ADE都是等腰直角三角形,
∴AB=AC,AD=AE,
∵四边形ABFD是平行四边形,
∴AD=BF,AD∥BF,
∴BF=AE,
∵AD∥BF,
∴∠DAB+∠FBA=180°,
∵∠DAE=∠BAC=90°,
∴∠DAB+∠EAC=180°,
∴∠EAC=∠FBA,
在△EAC和△FBA中,
∵
,
∴△EAC≌△FBA(SAS),
∴EC=AF,∠AFB=∠AEC,
延长FA交EC于G,
∵AD∥FB,
∴∠AFB=∠DAF,
∴∠DAF=∠AEC,
∵∠DAE=90°,
∴∠DAF+∠EAG=90°,
∴∠AEC+∠EAG=90°,
∴∠AGE=90°,
∴AF⊥BC;
(2)如图2,结论仍然成立,理由是: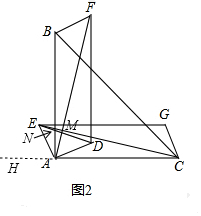
同理得:AB=AC,BF=AE,
作射线CA至H,则∠HAE+∠EAC=180°,
∵BF∥AD,
∴∠FBA+∠BAD=180°,
∵∠BAH=∠EAD=90°,
∴∠HAE+∠EAB=90°,∠BAD+∠EAB=90°,
∴∠HAE=∠BAD,
∴∠EAC=∠FBA,
∴△EAC≌△FBA,
∴AF=EC,∠BAF=∠ECA,
设CE与AB交于N,AF与EC交于点M,
∵∠BAC=90°,
∴∠ECA+∠ANC=90°,
∴∠BAF+∠ANC=90°,
∴∠AME=90°,
∴AF⊥EC.
 证明:(1)如图1,∵△ABC与△ADE都是等腰直角三角形,
证明:(1)如图1,∵△ABC与△ADE都是等腰直角三角形,∴AB=AC,AD=AE,
∵四边形ABFD是平行四边形,
∴AD=BF,AD∥BF,
∴BF=AE,
∵AD∥BF,
∴∠DAB+∠FBA=180°,
∵∠DAE=∠BAC=90°,
∴∠DAB+∠EAC=180°,
∴∠EAC=∠FBA,
在△EAC和△FBA中,
∵
|
∴△EAC≌△FBA(SAS),
∴EC=AF,∠AFB=∠AEC,
延长FA交EC于G,
∵AD∥FB,
∴∠AFB=∠DAF,
∴∠DAF=∠AEC,
∵∠DAE=90°,
∴∠DAF+∠EAG=90°,
∴∠AEC+∠EAG=90°,
∴∠AGE=90°,
∴AF⊥BC;
(2)如图2,结论仍然成立,理由是:

同理得:AB=AC,BF=AE,
作射线CA至H,则∠HAE+∠EAC=180°,
∵BF∥AD,
∴∠FBA+∠BAD=180°,
∵∠BAH=∠EAD=90°,
∴∠HAE+∠EAB=90°,∠BAD+∠EAB=90°,
∴∠HAE=∠BAD,
∴∠EAC=∠FBA,
∴△EAC≌△FBA,
∴AF=EC,∠BAF=∠ECA,
设CE与AB交于N,AF与EC交于点M,
∵∠BAC=90°,
∴∠ECA+∠ANC=90°,
∴∠BAF+∠ANC=90°,
∴∠AME=90°,
∴AF⊥EC.
看了 如图,△ABC与△ADE都是...的网友还看了以下:
矩形ABCD绕点A顺时针旋转至矩形AEFG,使B点正好落在CD上的点E处,连BE.1 求证 角BA 2020-05-16 …
今天刚考完的2010年全国数学竞赛,最后一道题,如图,已知四边形ABCD中 AC平分∠BAD AC 2020-05-16 …
在线段AB的同侧作射线AM和BN,若∠MAB与∠NBA的平分线分别交射线BN,AM于点E,F,AE 2020-06-08 …
如图1,将矩形ABCD绕点A顺时针旋转至矩形B点正好落在CD上的点E处,连结BE.(1)求证:∠B 2020-06-20 …
如图所示,将矩形ABCD沿AF折叠,使点D落在BC边的点E处,过点E作EG∥CD交AF于点G,连接 2020-07-10 …
若函数f(x)在R上可导,且f(x)>f'(x),当a>b时,下列不等式成立的是A.e^af(若函 2020-07-29 …
如图,在Rt△ABC中,∠B=90°,点E是AC的中点,AC=2AB,∠BAC的平分线AD交BC于 2020-07-30 …
如图,点E在正方形ABCD的边BC上,将△ABE沿直线AE折叠,使点B落在正方形内点P处,延长EP 2020-07-31 …
在等腰三角形abc中AB=AC=4,点D是BC的中点,点E,F分别在边AB,AC滑动,且E、F分别不 2020-12-23 …
给出3个关系式,2个为条件,一个为结论.快要交了.有空我请吃饭.三角形ADF和三角形BCE中,角A= 2020-12-23 …