早教吧作业答案频道 -->数学-->
如图1,将△ABC纸片沿中位线EH折叠,使点A对称点D落在BC边上,再将纸片分别沿等腰△BED和等腰△DHC的底边上的高线EF,HG折叠,折叠后的三个三角形拼合形成一个矩形,类似地,对多边形进
题目详情
如图1,将△ABC纸片沿中位线EH折叠,使点A对称点D落在BC边上,再将纸片分别沿等腰△BED和等腰△DHC的底边上的高线EF,HG折叠,折叠后的三个三角形拼合形成一个矩形,类似地,对多边形进行折叠,若翻折后的图形恰能合成一个无缝隙,无重叠的矩形,这样的矩形称为叠合矩形.
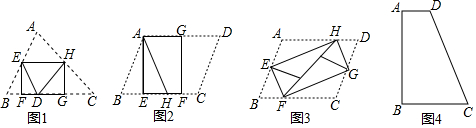
(1)将▱ABCD纸片按图2的方式折叠成一个叠合矩形AEFG,则操作形成的折痕分别是线段___,___;S矩形AEFG:S▱ABCD=___.
(2)如图4,四边形ABCD纸片满足AD∥BC,AD<BC,AB⊥BC,AB=8,CD=10,小明把该纸片折叠,得到叠合正方形,请你帮助画出叠合正方形的示意图,并求出AD、BC的长.

(1)将▱ABCD纸片按图2的方式折叠成一个叠合矩形AEFG,则操作形成的折痕分别是线段___,___;S矩形AEFG:S▱ABCD=___.
(2)如图4,四边形ABCD纸片满足AD∥BC,AD<BC,AB⊥BC,AB=8,CD=10,小明把该纸片折叠,得到叠合正方形,请你帮助画出叠合正方形的示意图,并求出AD、BC的长.
▼优质解答
答案和解析
(1)根据题意得:操作形成的折痕分别是线段AE、GF;
由折叠的性质得:△ABE≌△AHE,四边形AHFG≌四边形DCFG,
∴△ABE的面积=△AHE的面积,四边形AHFG的面积=四边形DCFG的面积,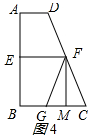
∴S矩形AEFG=
S▱ABCD,
∴S矩形AEFG:S▱ABCD=1:2;
故答案为:AE,GF,1:2;
(2)有两种折法,如图4、图5所示:
折法1中,如图4所示:
由折叠的性质得:AD=BG,AE=BE=
AB=4,CF=DF=
CD=5,GM=CM,∠FMC=90°,
∵四边形EFMB是叠合正方形,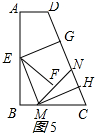
∴BM=FM=4,
∴GM=CM=
=
=3,
∴AD=BG=BM-GM=1,BC=BM+CM=7;
折法2中,如图5所示:
由折叠的性质得:四边形EMHG的面积=
梯形ABCD的面积,AE=BE=
AB=4,DG=NG,NH=CH,BM=FM,MC=CN,
∴GH=
CD=5,
∵四边形EMHG是叠合正方形,
∴EM=GH=5,正方形EMHG的面积=52=25,
∵∠B=90°,
∴FM=BM=
=3,
设AD=x,则MN=FM+FN=3+x,
∵梯形ABCD的面积=
(AD+BC)×8=2×25,
∴AD+BC=
,
∴BC=
-x,
∴MC=BC-BM=
-x-3,
∵MN=MC,
∴3+x=
-x-3,
解得:x=
,
∴AD=
,BC=
-
=
.
由折叠的性质得:△ABE≌△AHE,四边形AHFG≌四边形DCFG,
∴△ABE的面积=△AHE的面积,四边形AHFG的面积=四边形DCFG的面积,
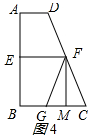
∴S矩形AEFG=
| 1 |
| 2 |
∴S矩形AEFG:S▱ABCD=1:2;
故答案为:AE,GF,1:2;
(2)有两种折法,如图4、图5所示:
折法1中,如图4所示:
由折叠的性质得:AD=BG,AE=BE=
| 1 |
| 2 |
| 1 |
| 2 |
∵四边形EFMB是叠合正方形,

∴BM=FM=4,
∴GM=CM=
| CF2-FM2 |
| 52-42 |
∴AD=BG=BM-GM=1,BC=BM+CM=7;
折法2中,如图5所示:
由折叠的性质得:四边形EMHG的面积=
| 1 |
| 2 |
| 1 |
| 2 |
∴GH=
| 1 |
| 2 |
∵四边形EMHG是叠合正方形,
∴EM=GH=5,正方形EMHG的面积=52=25,
∵∠B=90°,
∴FM=BM=
| 52-42 |
设AD=x,则MN=FM+FN=3+x,
∵梯形ABCD的面积=
| 1 |
| 2 |
∴AD+BC=
| 25 |
| 2 |
∴BC=
| 25 |
| 2 |
∴MC=BC-BM=
| 25 |
| 2 |
∵MN=MC,
∴3+x=
| 25 |
| 2 |
解得:x=
| 13 |
| 4 |
∴AD=
| 13 |
| 4 |
| 25 |
| 2 |
| 13 |
| 4 |
| 37 |
| 4 |
看了如图1,将△ABC纸片沿中位线...的网友还看了以下:
一张圆形纸片,直径10厘米,对折再对折后,得到一个新的图形(如图),计算这个新图形的周长. 2020-04-26 …
折叠矩形纸片ABCD先折出折狠(对角线),再折叠AD边与对角线BD重合,得折痕DG.若AB=2,B 2020-05-16 …
如图,折叠矩形纸ABCD,先折出折痕对角线BD,在折叠,使AD落在对角线BD上,得折痕DG.若AB 2020-05-21 …
将一张长方形的纸对折,如图所示可得到一条折痕(图中虚线);继续对折,对折时每次折痕与上次的折痕保持 2020-07-19 …
将一个长方形纸片连续对折,对折的次数越多,折痕的条数也就越多.如第一次对折后,有1条折痕,第2次对折 2020-11-19 …
将一张长方形的纸对折一次(如图),可以得到一条折痕(图中虚线),继续对折,对折时每次折痕与上次的折痕 2020-12-05 …
将一张长方形的纸对折,如图所示可得到一条折痕(图中虚线).继续对折,对折时每次折痕与上次的折痕保持平 2020-12-05 …
如图所示,将一张长方形的纸对折,可得一条折痕(图中虚线),继续对折,对折时每次的折痕与上次的折痕保持 2020-12-05 …
将一张长方形的纸对折,如图所示,可得到一条折痕(图中虚线),继续对折,对折时每次折痕与上次的折痕保持 2020-12-05 …
一张正方形的纸,沿对折线对折后,在得到的纸上随意剪出一个花纹,打开纸后得到的图案至少有一条对称轴,如 2020-12-08 …