早教吧作业答案频道 -->数学-->
如图,已知抛物线y2=4x,过点P(2,0)作斜率分别为k1,k2的两条直线,与抛物线相交于点A、B和C、D,且M、N分别是AB、CD的中点(1)若k1+k2=0,AP=2PB,求线段MN的长;(2)若k1•k2=-1,求△PMN
题目详情
如图,已知抛物线y2=4x,过点P(2,0)作斜率分别为k1,k2的两条直线,与抛物线相交于点A、B和C、D,且M、N分别是AB、CD的中点
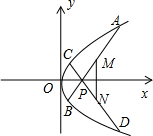
(1)若k1+k2=0,
=2
,求线段MN的长;
(2)若k1•k2=-1,求△PMN面积的最小值.

(1)若k1+k2=0,
| AP |
| PB |
(2)若k1•k2=-1,求△PMN面积的最小值.
▼优质解答
答案和解析
(1)设A(x1,y1),B(x2,y2),不妨设y1>0,则
设直线AB的方程为y=k1(x-2),代入y2=4x,可得y2-
y-8=0
∴y1+y2=
,y1y2=-8,
∵
=2
,∴y1=-2y2,∴y1=4,y2=-2,
∴yM=1,
∵k1+k2=0,
∴线段AB和CD关于x轴对称,
∴线段MN的长为2;
(2)∵k1•k2=-1,∴两直线互相垂直,
设AB:x=my+2,则CD:x=-
y+2,
x=my+2代入y2=4x,得y2-4my-8=0,
则y1+y2=4m,y1y2=-8,
∴M(2m2+2,2m).
同理N(
+2,-
),
∴|PM|=2|m|•
,|PN|=
•
,|
∴S△PMN=
|PM||PN|=
(m2+1)=2(|m|+
)≥4,
当且仅当m=±1时取等号,
∴△PMN面积的最小值为4.
设直线AB的方程为y=k1(x-2),代入y2=4x,可得y2-
| 4 |
| k1 |
∴y1+y2=
| 4 |
| k1 |
∵
| AP |
| PB |
∴yM=1,
∵k1+k2=0,
∴线段AB和CD关于x轴对称,
∴线段MN的长为2;
(2)∵k1•k2=-1,∴两直线互相垂直,
设AB:x=my+2,则CD:x=-
| 1 |
| m |
x=my+2代入y2=4x,得y2-4my-8=0,
则y1+y2=4m,y1y2=-8,
∴M(2m2+2,2m).
同理N(
| 2 |
| m2 |
| 2 |
| m |
∴|PM|=2|m|•
| m2+1 |
| 2 |
| m2 |
| m2+1 |
∴S△PMN=
| 1 |
| 2 |
| 1 |
| |m| |
| 1 |
| |m| |
当且仅当m=±1时取等号,
∴△PMN面积的最小值为4.
看了如图,已知抛物线y2=4x,过...的网友还看了以下:
(2011•青岛模拟)(1)某原子mnX经过2次α衰变,4次β衰变后变为qpY,那么n与p的数学关 2020-04-07 …
已知X~B(n,p),E(X)=8,D(X)=1.6,则n与p的值分别是[]A.n=100,p=0 2020-05-13 …
设服从二项分布B~(n,p)的随机变量ξ的期望和方差分别是2.4与1.44,则二项分布的参数n、p 2020-05-15 …
设服从二项分布B~(n,p)的随机变量ξ的期望和方差分别是2.4与1.44,则二项分布的参数n、p 2020-05-15 …
1.对于可逆反应mA(g)+nB(g)pC(g)+qD(g),讨论他的转化率问题条件是恒温恒容,只 2020-06-04 …
∑[k=0,∞]C(k,N)C(n-k,M-N)=C(n,M)∑[k=0,n](1-p)^k=1/ 2020-07-16 …
已知:m+n=0,n+p=0,m+q=0,则()A.p与q相等B.m与n互为相反数C.m与n相等D 2020-07-30 …
已知△ABC的顶点A(1,0),点B在x轴上移动,|AB|=|AC|,且BC的中点在y轴上.(Ⅰ) 2020-07-31 …
已知随机变量η~B(n,p),且E(2η)=8,D(4η)=32,则n与p的值分别是()A.20与0 2020-11-02 …
二力比较吊装一钢梁,吊点位置不变,吊索与梁的夹角分别为60、45、30度,设斜索中拉力为N,总吊索拉 2020-11-11 …