如图，Rt△ABC中，∠BAC=90°，AB=3，AC=1，在△ABC内依次作等边三角形，使一边在AB上，另一个顶点在BC边上，依次作出的等边三角形分别是第1个为△AA1B1，第2个为△B1A2B2，第3个△B2A3B3，…，则

Question

如图，Rt△ABC中，∠BAC=90°，AB=

√(3)，AC=1，在△ABC内依次作等边三角形，使一边在AB上，另一个顶点在BC边上，依次作出的等边三角形分别是第1个为△AA₁B₁，第2个为△B₁A₂B₂，第3个△B₂A₃B₃，…，则第2017个等边三角形的边长为（　　）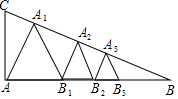

A.

(√(3))/(22018)

B.

(√(3))/(22017)

C.

(√(3))/(22016)

D.

(√(3))/(22015)

Answer 1

∵OB=√(3)，OC=1，
∴BC=2，
∴∠OBC=30°，∠OCB=60°．
而△AA₁B₁为等边三角形，∠A₁AB₁=60°，
∴∠COA₁=30°，则∠CA₁O=90°．
在Rt△CAA₁中，AA₁=(√(3))/(2)OC=(√(3))/(2)，
同理得：B₁A₂=(1)/(2)A₁B₁=(√(3))/(22)，
依此类推，第n个等边三角形的边长等于(√(3))/(2n)，
则第2017个等边三角形的边长为(√(3))/(22017)．
故选：B．