早教吧作业答案频道 -->数学-->
在直角坐标系中,有点A(0,1),B(5,3),点M、N在x轴上且MN=1,当四边形AMNB周长最短时,求点M、N的坐标.
题目详情
在直角坐标系中,有点A(0,1),B(5,3),点M、N在x轴上且MN=1,当四边形AMNB周长最短时,求点M、N的坐标.
▼优质解答
答案和解析
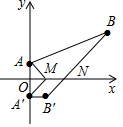 作点A关于x轴的对称点A′,则A′的坐标为(0,-1),把A′向右平移1个单位得到点B'(1,-1),连接BB′,与x轴交于点N,过A′作A′M∥B′N交x轴于M,如图,
作点A关于x轴的对称点A′,则A′的坐标为(0,-1),把A′向右平移1个单位得到点B'(1,-1),连接BB′,与x轴交于点N,过A′作A′M∥B′N交x轴于M,如图,
∴MA′=MA,
∵A′M∥B′N,
∴四边形AMNB为平行四边形,
∴MA′=NB′,
∴MA=NB′,
∴AM+BN=BB′,此时AM+BN最小,
而MN与AB的长一定,
∴此时四边形AMNB的周长最短.
设直线BB′的解析式为y=kx+b,
把B(5,3)、B'(1,-1)分别代入得
,
解得k=1,b=-2,
∴直线BB′的解析式为y=x-2,
令y=0,则x-2=0,
解得x=2,
∴N点坐标为(2,0),
∵MN=1,
∴M(1,0).
 作点A关于x轴的对称点A′,则A′的坐标为(0,-1),把A′向右平移1个单位得到点B'(1,-1),连接BB′,与x轴交于点N,过A′作A′M∥B′N交x轴于M,如图,
作点A关于x轴的对称点A′,则A′的坐标为(0,-1),把A′向右平移1个单位得到点B'(1,-1),连接BB′,与x轴交于点N,过A′作A′M∥B′N交x轴于M,如图,∴MA′=MA,
∵A′M∥B′N,
∴四边形AMNB为平行四边形,
∴MA′=NB′,
∴MA=NB′,
∴AM+BN=BB′,此时AM+BN最小,
而MN与AB的长一定,
∴此时四边形AMNB的周长最短.
设直线BB′的解析式为y=kx+b,
把B(5,3)、B'(1,-1)分别代入得
|
解得k=1,b=-2,
∴直线BB′的解析式为y=x-2,
令y=0,则x-2=0,
解得x=2,
∴N点坐标为(2,0),
∵MN=1,
∴M(1,0).
看了在直角坐标系中,有点A(0,1...的网友还看了以下:
如图,正方形ABCD的边长为2,且边与坐标轴平行,已知点B的坐标是(5,5),欲使抛物线y=ax^ 2020-04-27 …
一道关于三角形数学题的选择题,请简单的说明一下为什么小明有甲乙两块三角板,它们的厚度相同,甲三角形 2020-05-13 …
1.如果菱形的周长为20,两菱角的比为1;2,问⑴较短对角线的长是多少?⑵一组对边的距离是多少?2 2020-05-13 …
已知椭圆的中心在坐标原点O,焦点焦距为2,且椭圆的短轴两端点和两焦点所组成的四边形为正方形,1求椭 2020-05-15 …
已知角abcd是平行四边形,ef是对角线上的两,且be=df,连接ae.af.ce.cf;判断四边 2020-05-16 …
(2011•衢州)木工师傅可以用角尺测量并计算出圆的半径r,用角尺的较短边紧靠⊙O,并使较长边与⊙ 2020-05-17 …
木工师傅可以用角尺测量并计算出圆的半径r,用角尺的较短边紧靠⊙O,并使较长边与⊙O相切于点C,假设 2020-05-17 …
一个直角三角形的“短”的一个直角边为1.5米,其中一个角为47.74度.求这个直角三角形其他两条边 2020-05-20 …
当45°<θ<90°时,下列各式中正确的是().A.tanθ>cosθ>sinθB.sinθ>co 2020-06-16 …
三角形较短的两条边较短的两条边和等于第三条边,能组成三角形吗 2020-06-17 …