早教吧作业答案频道 -->数学-->
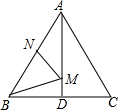
如图,在等边△ABC中,AB=2,N为AB上一点,且AN=1,∠BAC的平分线交BC于点D,M是AD上的动点,连结BM、MN,则BM+MN的最小值是.
题目详情
如图,在等边△ABC中,AB=2,N为AB上一点,且AN=1,∠BAC的平分线交BC于点D,M是AD上的动点,连结BM、MN,则BM+MN的最小值是___.

▼优质解答
答案和解析
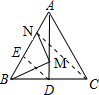 连接CN,与AD交于点M.则CN就是BM+MN的最小值.
连接CN,与AD交于点M.则CN就是BM+MN的最小值.
取BN中点E,连接DE.
∵等边△ABC的边长为2,AN=1,
∴BN=AC-AN=2-1=1,
∴BE=EN=AN=1,
又∵AD是BC边上的中线,
∴DE是△BCN的中位线,
∴CN=2DE,CN∥DE,
又∵N为AE的中点,
∴M为AD的中点,
∴MN是△ADE的中位线,
∴DE=2MN,
∴CN=2DE=4MN,
∴CM=
CN.
在直角△CDM中,CD=
BC=1,DM=
AD=
,
∴CM=
=
,
∴CN=
×
=
.
∵BM+MN=CN,
∴BM+MN的最小值为
.
故答案为
 连接CN,与AD交于点M.则CN就是BM+MN的最小值.
连接CN,与AD交于点M.则CN就是BM+MN的最小值.取BN中点E,连接DE.
∵等边△ABC的边长为2,AN=1,
∴BN=AC-AN=2-1=1,
∴BE=EN=AN=1,
又∵AD是BC边上的中线,
∴DE是△BCN的中位线,
∴CN=2DE,CN∥DE,
又∵N为AE的中点,
∴M为AD的中点,
∴MN是△ADE的中位线,
∴DE=2MN,
∴CN=2DE=4MN,
∴CM=
| 3 |
| 4 |
在直角△CDM中,CD=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
∴CM=
| CD2+MD2 |
3
| ||
| 4 |
∴CN=
| 4 |
| 3 |
3
| ||
| 4 |
| 3 |
∵BM+MN=CN,
∴BM+MN的最小值为
| 3 |
故答案为
| 3 |
看了如图,在等边△ABC中,AB=...的网友还看了以下:
已知椭圆的左焦点为F1(-c,0),A(-a,0)B(b,0)是两个顶点,如果F1到直线AB的距离 2020-05-13 …
如图,DC//AB,角BAD和角ADC的角(急)如图,DC//AB,角BAD和角ADC的角平分线相 2020-05-16 …
若a分之1+b分之1=a+b分之1,则a分之b+b分之a的值为多少? 这道题中为什么(a+b)²= 2020-05-16 …
相似三角形 1.已知,如图,AB⊥BD于B,CD⊥BD于D,连接AD、BC它们相交于E,EF⊥BD 2020-05-17 …
两个连续奇数的倒数相差一百九十分之二,这两个奇数分别是多少?提示::7/1-8/1=56/1=7/ 2020-07-18 …
如图所示,AB垂直BC,DC垂直BC,垂足分别为点B,C{1}当AB=4,DC=1,BC=4时,在 2020-07-24 …
如图,点o是线段ab的中点,AB=24cm.(1)如果M,N亮点把线段AB分成1:4:3三部分,求 2020-07-25 …
根据绝对值得定义,回答下面的问题,1:如果|a|分之a等于1,那么a0;2:如果|a|分之a等于- 2020-08-01 …
如果ab都是正数.且a不等于b求证:根号b分之a+根号a分之b>根号a+根号b?(有些文字手机上看 2020-08-01 …
如图,点C把线段AB分成两条线段AC和BC,如果ACAB=BCAC,那么下列说法错误的是()A.线 2020-08-02 …