早教吧作业答案频道 -->数学-->
计算:(1);(2)(3)1+2i+3i2+…+1000i999
题目详情
计算:(1)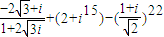 ;
;
(2)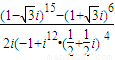
(3)1+2i+3i 2 +…+1000i 999
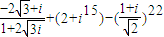 ;
;(2)
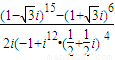
(3)1+2i+3i 2 +…+1000i 999
▼优质解答
答案和解析
分析:
利用ω3=3=1,ω+=-1,ω=1,ω2=,2=ω,|ω|=||=1,1+ω+ω2=0,1++2=0这些性质中(ω=-+i);(1±i)2=±2i,,解答(1)(2).利用i的幂的周期性解答(3).
(1)原式=+(2-i)-=i+2-i-(-i)=2+i(2)原式===(3)解法1:原式=(1+2i-3-4i)+(5+6i-7-8i)++(997+998i-999-1000i)=250(-2-2i)=-500-500i=-1000=-1000解法2:设S=1+2i+3i2++1000i999,则iS=i+2i2+3i3++999i999+1000i1000,∴(1-i)S=1+i+i2++i999-1000i1000=-1000=-1000∴S==-500-500i.
点评:
(1)计算时要注意提取公因式,要注意利用i的幂的周期性.(2)重视利用ω3=3=1,ω+=-1,ω=1,ω2=,2=ω,|ω|=||=1,1+ω+ω2=0,1++2=0这些性质(ω=-+i);要记住常用的数据:(1±i)2=±2i,,.(3)充分利用i的幂的周期性进行组合,注意利用等比数列求和的方法.
分析:
利用ω3=3=1,ω+=-1,ω=1,ω2=,2=ω,|ω|=||=1,1+ω+ω2=0,1++2=0这些性质中(ω=-+i);(1±i)2=±2i,,解答(1)(2).利用i的幂的周期性解答(3).
(1)原式=+(2-i)-=i+2-i-(-i)=2+i(2)原式===(3)解法1:原式=(1+2i-3-4i)+(5+6i-7-8i)++(997+998i-999-1000i)=250(-2-2i)=-500-500i=-1000=-1000解法2:设S=1+2i+3i2++1000i999,则iS=i+2i2+3i3++999i999+1000i1000,∴(1-i)S=1+i+i2++i999-1000i1000=-1000=-1000∴S==-500-500i.
点评:
(1)计算时要注意提取公因式,要注意利用i的幂的周期性.(2)重视利用ω3=3=1,ω+=-1,ω=1,ω2=,2=ω,|ω|=||=1,1+ω+ω2=0,1++2=0这些性质(ω=-+i);要记住常用的数据:(1±i)2=±2i,,.(3)充分利用i的幂的周期性进行组合,注意利用等比数列求和的方法.
看了计算:(1);(2)(3)1+...的网友还看了以下:
S=(1+1/1*2+(2+1/2*3)+(3+1/3*4)+...+(20+1/20*21)S= 2020-04-27 …
上面写不下,我写在下面填符号1.(1)1/2()0.4()3/10()0.1=1(2)1/2()0 2020-05-13 …
数列{an}各项是1或3,且在第k个1和第k+1个1之间有2k-1个3,即1,3,1,3,3,3, 2020-05-16 …
谁能告诉我这个算式的简化公式(1+x)(1+x^2)(1+x^3)(1+x^4)(1+x^5)(1 2020-05-17 …
1+2+3+n=2分之1n(n+1),n是正整数,研究1*2+2*3+你(n+1),观察1*2=3 2020-05-20 …
天才进1,1,2,1,2,1,2,3,3,1,3,2,1,2,3,3,1,3,2,1,3,2,3, 2020-05-21 …
49.7-[-23/3/4+(18.7-25.25)]12+1又3/4-8又5/12-6.75-( 2020-06-04 …
(1+1/2+1/3+1/5)*(1/2+1/3+1/5+1/7)-(1+1/2+1/3+1/5+ 2020-06-08 …
(2012•开封一模)下列表示对应化学反应的离子方程式正确的是()A.用碘酸钾氧化酸性溶液中的碘化钾 2020-11-01 …
(2012•河北模拟)下列离子方程式正确的是()A.用KIO3氧化酸性溶液中的KI:5I-+IO-3 2020-11-01 …