（本题满分9分）如图，平面直角坐标系中，过点C（28，28）分别作x轴、y轴的垂线，垂足分别为B、A，一次函数y=x+3的图像分别与x轴和CB交于点D、E，点P是DE中点，连接AP.（1）求

Question

（本题满分9分）如图，平面直角坐标系中，过点C（28，28）分别作x轴、y轴的垂线，垂足分别为B、A，一次函数y=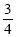 x+3的图像分别与x轴和CB交于点D、E，点P 是DE中点，连接AP.

（1）求证：△ADO≌△AEC；

（2）求AP的长．

Answer 1

(1)见解析；(2)AP=20.

分 析：
根据图先求出D、E的坐标，然后再根据全等三角形的判定定理即可得出结论；(2)由(1)的结论，即可得出∠DAE=90°，再由勾股定理得出DE的长，然后利用中点的性质即可得出AP的值.试题
解析：
（1） 由题意可得：D（—4 0），E（28 24）在△ADO与△AEC中∴△ADO≌△AEC. 由△ADO≌△AEC全等可知：∠EAC=∠DAO， ∴∠DAE=90°. ∵P为DE中点，∴AP=DE在Rt△DBE中，DE2=BD2+BE2=242+322=1600∴DE=40， ∴AP=20.
考点：
全等三角形的性质和判定；勾股定理.