早教吧作业答案频道 -->数学-->
如图,将平行四边形ABCD沿对角线BD进行折叠,折叠后点C落在点F处,DF交AB于点E.(1)求证:三角形DEB是等腰三角形;(2)判断AF与BD是否平行,并说明理由.
题目详情
如图,将平行四边形ABCD沿对角线BD进行折叠,折叠后点C落在点F处,DF交AB于点E.
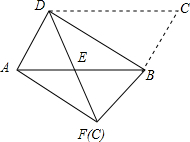
(1)求证:三角形DEB是等腰三角形;
(2)判断AF与BD是否平行,并说明理由.

(1)求证:三角形DEB是等腰三角形;
(2)判断AF与BD是否平行,并说明理由.
▼优质解答
答案和解析
(1)由折叠可知:∠CDB=∠EDB,
∵四边形ABCD是平行四边形,
∴DC∥AB,
∴∠CDB=∠EBD,
∴∠EDB=∠EBD,
∴△BDE是等边三角形;
(2)AF∥DB;
∵∠EDB=∠EBD,
∴DE=BE,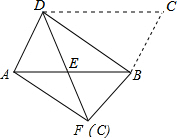
由折叠可知:DC=DF,
∵四边形ABCD是平行四边形,
∴DC=AB,
∴DF=AB,
∴AE=EF,
∴∠EAF=∠EFA,
在△BED中,∠EDB+∠EBD+∠DEB=180°,
∴2∠EDB+∠DEB=180°,
同理,在△AEF中,2∠EFA+∠AEF=180°,
∵∠DEB=∠AEF,
∴∠EDB=∠EFA,
∴AF∥DB.
∵四边形ABCD是平行四边形,
∴DC∥AB,
∴∠CDB=∠EBD,
∴∠EDB=∠EBD,
∴△BDE是等边三角形;
(2)AF∥DB;
∵∠EDB=∠EBD,
∴DE=BE,

由折叠可知:DC=DF,
∵四边形ABCD是平行四边形,
∴DC=AB,
∴DF=AB,
∴AE=EF,
∴∠EAF=∠EFA,
在△BED中,∠EDB+∠EBD+∠DEB=180°,
∴2∠EDB+∠DEB=180°,
同理,在△AEF中,2∠EFA+∠AEF=180°,
∵∠DEB=∠AEF,
∴∠EDB=∠EFA,
∴AF∥DB.
看了如图,将平行四边形ABCD沿对...的网友还看了以下:
设A是n阶矩阵A^2=E,证明r(A+E)+r(A-E)=n,的一步证明过程不懂由A^2=E,得A 2020-05-14 …
如图E、F、G、H分别是空间四边形ABCD的边AB、BC、CD、DA的中点.(1)求证:四边形EF 2020-05-15 …
如图,在平行四边形ABCD中,M,N分别是AB,CD上的点,AM=CN,E,F是AC上的点,AE= 2020-05-16 …
已知ABCD-A1B1C1D1是棱长为3的正方体,点E在AA1上,点F在CC1上,且AE=FC1= 2020-05-16 …
如图,平行四边形ABCD中,AE=CG,DH=BF,连结E,F,G,H,E,则四边形EFHG是?如 2020-05-16 …
如图,两张等宽的纸条交叉重叠在一起,重叠的部分ABCD是菱形吗?求证:(1)四边形ABCD是平行四 2020-05-16 …
如图,在平行四边形ABCD中,点E、F分别是AB、DC的中点,AF与DE交于点G,BF与CE交于点 2020-05-17 …
大家看看我这个矩阵的证明哪里有问题已知A,B为n阶方阵,且B=B^2,A=B+E,证明A可逆,并求 2020-06-09 …
如图,在平面直角坐标系中,有平行四边形ABCD,且A(-1,0),B(0,3),C(3,0),BD 2020-06-13 …
空间四边形ABCD中,E,F是AB,AD的中点,G,H在BC,DC上,且BG:GC=DH:HC=1 2020-06-27 …