早教吧作业答案频道 -->数学-->
如图①,已知A(a,0),B(0,b),且a,b满足a2-8a+b2-8b=-32.(1)求A,B两点的坐标;(2)若点C在第一象限内的一点,且∠OCB=45°,过A作AD⊥OC于D点,求证:AD=CD;(3)如图②,若已知E(1
题目详情
如图①,已知A(a,0),B(0,b),且a,b满足a2-8a+b2-8b=-32.
(1)求A,B两点的坐标;
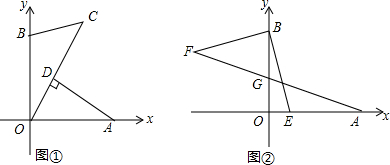
(2)若点C在第一象限内的一点,且∠OCB=45°,过A作AD⊥OC于D点,求证:AD=CD;
(3)如图②,若已知E(1,0),连接BE,过B作BF⊥BE且BF=BE,连接AF交y轴于G点,求G点的坐标.
(1)求A,B两点的坐标;
(2)若点C在第一象限内的一点,且∠OCB=45°,过A作AD⊥OC于D点,求证:AD=CD;
(3)如图②,若已知E(1,0),连接BE,过B作BF⊥BE且BF=BE,连接AF交y轴于G点,求G点的坐标.

▼优质解答
答案和解析
(1) ∵a2-8a+b2-8b=-32,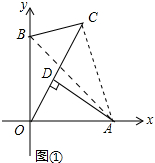
∴(a2-8a+16)+(b2-8b+16)=0,
∴(a-4)2+(b-4)2=0,
∵(a-4)2≥0,(b-4)2≥0,
∴a=b=4,
∴点A坐标为(4,0),点B坐标为(0,4).
(2)证明:∵点A坐标为(4,0),点B坐标为(0,4),
∴OA=OB,
∴∠OAB=∠OBA=45°,
∵∠BCO=45°,
∴∠BCO=∠BAO,
∴O、A、C、B四点共圆,
∴∠AOB+∠BCA=180°,
∵∠AOB=90°,
∴∠BCA=90°,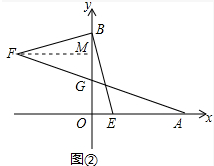
∴∠DCA=90°-∠BCA=45°,
∵AD⊥CD,
∴∠ADC=90°,∠DCA=∠DAC=45°,
∴DC=DA.
(3) 作FM⊥OB于M,
∵∠FBM+∠OBE=90°,∠OBE+∠OEB=90°,
∴∠FBM=∠BEO,
在△FBM和△BEO中,
,
∴△BFM≌△EBO,
∴FM=BO=AO,BM=OE=1,OM=3,
∵FM∥AO,
∴∠FMG=∠AOG,
在△FMG和△AOG中,
,
∴△FMG≌△AOG,
∴MG=OG=
OM=
,
∴点M坐标(0,
).

∴(a2-8a+16)+(b2-8b+16)=0,
∴(a-4)2+(b-4)2=0,
∵(a-4)2≥0,(b-4)2≥0,
∴a=b=4,
∴点A坐标为(4,0),点B坐标为(0,4).
(2)证明:∵点A坐标为(4,0),点B坐标为(0,4),
∴OA=OB,
∴∠OAB=∠OBA=45°,
∵∠BCO=45°,
∴∠BCO=∠BAO,
∴O、A、C、B四点共圆,
∴∠AOB+∠BCA=180°,
∵∠AOB=90°,
∴∠BCA=90°,

∴∠DCA=90°-∠BCA=45°,
∵AD⊥CD,
∴∠ADC=90°,∠DCA=∠DAC=45°,
∴DC=DA.
(3) 作FM⊥OB于M,
∵∠FBM+∠OBE=90°,∠OBE+∠OEB=90°,
∴∠FBM=∠BEO,
在△FBM和△BEO中,
|
∴△BFM≌△EBO,
∴FM=BO=AO,BM=OE=1,OM=3,
∵FM∥AO,
∴∠FMG=∠AOG,
在△FMG和△AOG中,
|
∴△FMG≌△AOG,
∴MG=OG=
| 1 |
| 2 |
| 3 |
| 2 |
∴点M坐标(0,
| 3 |
| 2 |
看了如图①,已知A(a,0),B(...的网友还看了以下:
给出一个数n,n的约数的个数用一个记号b(n)表示,求:1.A(42).2.B(42).3.如A( 2020-05-13 …
如图,在直角梯形ABCD中,AB∥CD,AB⊥BC,以BC为直径的O与AD相切,点E为AD的中点, 2020-05-14 …
如图,将正方形纸片ABCD折叠,使点B落在CD边上一点E(不与点C,D重合),压平后得到折痕MN. 2020-05-16 …
r=6求cr=2.3求cr=2/5求cd=3.6求cd=2/3求cd=3/5求cc=1r=6求cr 2020-06-07 …
亲们费心了╭(╯3╰)╮如图,直线AD与BC、CD相交于A、D两点,EC、BF与AB、CD交点于E 2020-07-19 …
如图,如果∠1=∠3,那么根据,可得AB∥CD.(1)∠1的内错角是.(2)AB∥CD,∠1=30 2020-07-23 …
如图,半圆O的直径AD=12cm,AB,BC,CD分别与半圆O切于点A,E,D.(1)设AB=x, 2020-07-30 …
如图,在矩形ABCD中,AB=3,BC=4,P是边AD上一点(除端点A),过点A、B、P作○O(1 2020-07-30 …
如图在rt△abc中,AB是斜边,点P在中线CD上,AC=3,BC=4如图,在RT△ABC中,∠A 2020-07-30 …
请解答下列问题:(1)如图1,AB∥CD,试证明:∠B+∠D=∠BED.(2)已知:如图2,AB∥C 2020-11-03 …