早教吧作业答案频道 -->数学-->
如图,已知A(0,4),E(8,0),点P(a,0)是线段OE上的动点,点B为AP的中点,以BP为边向右边作正方形PBCD,过点B作BM⊥x轴于点M,过点D作DF⊥x轴于点F,连接DE.(1)判断DF,BM,MF之间的
题目详情
如图,已知A(0,4),E(8,0),点P(a,0)是线段OE上的动点,点B为AP的中点,以BP为边向右边作正方形PBCD,过点B作BM⊥x轴于点M,过点D作DF⊥x轴于点F,连接DE.
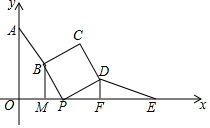
(1)判断DF,BM,MF之间的关系,并说明理由;
(2)求点D的坐标(用含a的代数式表示);
(3)当点P在线段OE(点O,点E除外)上运动时,设△PDE的面积为S,写出S与a的函数关系式,当点P运动到何处时,△PDE的面积最大,最大是多少?

(1)判断DF,BM,MF之间的关系,并说明理由;
(2)求点D的坐标(用含a的代数式表示);
(3)当点P在线段OE(点O,点E除外)上运动时,设△PDE的面积为S,写出S与a的函数关系式,当点P运动到何处时,△PDE的面积最大,最大是多少?
▼优质解答
答案和解析
(1)结论:MF=DF+BM.
理由:∵四边形ABCD是正方形,
∴PB=PD,∠BPD=90°,
∵BM⊥OE,DF⊥OE,
∴∠BMP=∠DFP=90°,
∵∠BPM+∠DPF=90°,∠MBP+∠BPM=90°,
∴∠MBP=∠DPF,
∴△PBM≌△DPF,
∴PM=DF,BM=PF,
∴MF=MP+PF=DF+BM.
(2)∵A(0,4),P(a,0),
∴OA=4,OP=a,
∵B为AP的中点,
∴B(
,2),BM=PF=2,OM=PM=DF=
a,
∴D(a+2,
).
(3)由题意S=
•PE•DF=
(8-a)•
a=
a(8-a)=-
(a-4)2+4,
∵-
<0,
∴a=4时,S有最大值4.
∴当P运动到P(4,0)时,△PDE的面积最大,最大面积为4.
理由:∵四边形ABCD是正方形,
∴PB=PD,∠BPD=90°,

∵BM⊥OE,DF⊥OE,
∴∠BMP=∠DFP=90°,
∵∠BPM+∠DPF=90°,∠MBP+∠BPM=90°,
∴∠MBP=∠DPF,
∴△PBM≌△DPF,
∴PM=DF,BM=PF,
∴MF=MP+PF=DF+BM.
(2)∵A(0,4),P(a,0),
∴OA=4,OP=a,
∵B为AP的中点,
∴B(
| a |
| 2 |
| 1 |
| 2 |
∴D(a+2,
| a |
| 2 |
(3)由题意S=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
∵-
| 1 |
| 4 |
∴a=4时,S有最大值4.
∴当P运动到P(4,0)时,△PDE的面积最大,最大面积为4.
看了如图,已知A(0,4),E(8...的网友还看了以下:
有含盐5%的盐水10千克,要用15千克的盐水和它混合,使混合后的盐水浓度不低于8%,且不高于14% 2020-05-13 …
有含盐5%的盐水10千克,要用15千克的盐水和它混合,使混合后的盐水浓度不低于8%,且不高于14% 2020-05-13 …
有含盐5%的盐水10千克,要用15千克的盐水和它混合,使混合后的盐水浓度不低于8%,且不高于14% 2020-05-13 …
若P(A)=0.6,P(B)=0.8,P(A∪B)最大值为1,最小值为0.8,为什么?还有就是P( 2020-06-14 …
如图,在Rt△ABC中,∠BAC=90°(1)先作∠ACB的平分线交AB边于点P,再以点P为圆心, 2020-06-22 …
自考.工程经济学.(F/P,8%,5)=1.469(P/F,8%,5)=0.6806(F/A,8% 2020-07-18 …
(2014•建邺区一模)如图,在△ABC中,AB=AC=42,BC=8.⊙A的半径为2,动点P从点 2020-07-21 …
某工程项目计划3年完成,3年中每年年初分别贷款1000万元,年利率8%,若建成后分三年每年年末等额 2020-07-23 …
如图所示.⊙O的半径为5厘米.点P是⊙O外一点,OP=8厘米.求:(1)以P为圆心作⊙P与⊙O外切, 2020-11-26 …
大学概率课后习题提问!已知P(A)=1/2,若P(AB)=1/8,求P(A-B)(A乘以杠B的意思) 2020-12-13 …