如图所示,一根弹簧,一端固定在竖直墙上,在弹性限度内用手水平向右拉伸弹簧的另一端,下列有关“弹簧形变产生的力”描述正确的是()A.弹簧对手的拉力B.手对弹簧的拉力C.
如图所示,一根弹簧,一端固定在竖直墙上,在弹性限度内用手水平向右拉伸弹簧的另一端,下列有关“弹簧形变产生的力”描述正确的是( )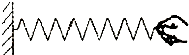
A. 弹簧对手的拉力
B. 手对弹簧的拉力
C. 墙对弹簧的拉力
D. 以上说法都正确
故选:A.
关于对公客户经理的任职和晋升年限规定,下列说法错误的是()。A.升任客户经理需3年及以上金融工 2020-05-27 …
这道积分怎么证明设函数f(x)以T为周期,证明a+TT∫f(x)dx=∫f(x)dx(a为常数)a 2020-07-09 …
利用定积分定义计算下列积分!是求积分,不是定积分!1.:∫(e^x)dx,上限是1,下限是0;求此 2020-07-23 …
用matlab求定积分的上限b的值定积分l=∫(x^2+y^2+z^2)^(1/2)*xd(t)上 2020-07-24 …
定积分几何意义根据定积分的几何意义说明下列等式:设f(x)是周期为T的周期函数,且在任意有限区间上 2020-07-31 …
定积分问题.1、∫(cos2x)^8dx积分上限为π/4,下限为0.2、设f(x)在a,b上连续, 2020-07-31 …
高数中-中有一例题.个人感觉有点问题(其中的一部分是)对∫0积分上限)-a积分下限)f(x)dx作 2020-07-31 …
关于积分上下限的问题关于定积分∫[a->b]]的几何意义,若f(x)>0则定积分表示x=ax=bf 2020-07-31 …
高数定积分证明题y(x)在[a,b]上连续,在(a,b)上可导,证明:y(x)=定积分(上限u(x 2020-08-03 …
为什么牛顿莱布尼兹公式中不用加常数C?有点疑惑的问题~o(* ̄▽ ̄*)o牛顿莱布尼兹公式:b(上限) 2020-11-21 …