早教吧作业答案频道 -->数学-->
如图,点F在▱ABCD的对角线AC上,过点F、B分别作AB、AC的平行线相交于点E,连接BF,∠ABF=∠FBC+∠FCB.(1)求证:四边形ABEF是菱形;(2)若BE=5,AD=8,∠CBE=30°,求AC的长.
题目详情
如图,点F在▱ABCD的对角线AC上,过点F、B分别作AB、AC的平行线相交于点E,连接BF,∠ABF=∠FBC+∠FCB.
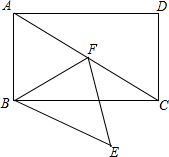
(1)求证:四边形ABEF是菱形;
(2)若BE=5,AD=8,∠CBE=30°,求AC的长.

(1)求证:四边形ABEF是菱形;
(2)若BE=5,AD=8,∠CBE=30°,求AC的长.
▼优质解答
答案和解析
(1)证明:∵EF∥AB,BE∥AF,
∴四边形ABEF是平行四边形.
∵∠ABF=∠FBC+∠FCB,∠AFB=∠FBC+∠FCB,
∴∠ABF=∠AFB,
∴AB=AF,
∴▱ABEF是菱形;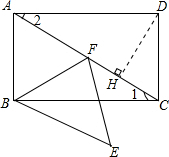
(2) 作DH⊥AC于点H,
∵∠CBE=30°,
∵BE∥AC,
∴∠1=∠CBE,
∵AD∥BC,
∴∠2=∠1,
∴∠2=∠CBE=30°,
Rt△ADH中,AH=AD•cos∠2=4
,
DH=AD•sin∠2=4,
∵四边形ABEF是菱形,
∴CD=AB=BE=5,
Rt△CDH中,CH=
=3,
∴AC=AH+CH=4
+3.
∴四边形ABEF是平行四边形.
∵∠ABF=∠FBC+∠FCB,∠AFB=∠FBC+∠FCB,
∴∠ABF=∠AFB,
∴AB=AF,
∴▱ABEF是菱形;

(2) 作DH⊥AC于点H,
∵∠CBE=30°,
∵BE∥AC,
∴∠1=∠CBE,
∵AD∥BC,
∴∠2=∠1,
∴∠2=∠CBE=30°,
Rt△ADH中,AH=AD•cos∠2=4
| 3 |
DH=AD•sin∠2=4,
∵四边形ABEF是菱形,
∴CD=AB=BE=5,
Rt△CDH中,CH=
| CD2-DH2 |
∴AC=AH+CH=4
| 3 |
看了如图,点F在▱ABCD的对角线...的网友还看了以下:
已知椭圆M:x2/a2+y2/3=1(a>0)的一个焦点为F(-1,0)已知椭圆M:x2/a2+y 2020-05-17 …
已知:0°C时等于32°F,100°C时等于212°F.求20°C时等于多少°F,90°F等于多少 2020-06-12 …
已知函数f(x-1)的图像与函数g(x)的图像关于直线y=x对称,且g(1)=2则:A,f(1)= 2020-06-27 …
如图,在直角坐标系中,点A坐标为(1,0),点B坐标为(0,1),E、F是线段AB上的两个动点,且 2020-07-21 …
在坐标平面中,直线y=x+5分别交x轴、y轴于A、B,直线y=-2x+20分别交x轴、y轴于C、D 2020-07-30 …
已知抛物线C:y2=2x的焦点为F,平行于x轴的两条直线l1,l2分别交C于A,B两点,交C的准线 2020-07-31 …
时间很赶,1.设函数y=x^2-3|x-1|-1的图像与x轴的焦点个数有()A.1个B.2个C.3个 2020-11-10 …
(2013•保定模拟)如图:AB是AB所对的弦,AB的中垂线CD分别交AB于C,交AB于D,AD的中 2020-11-12 …
高一数学试题若函数y=f(x)在x=a及x=b之间的一段图像可以近似地看作直线,a小于等于c小于等于 2020-12-08 …
若f(x)是R上的的偶函数且在0,+正无穷极)上是增函数,则下列成立的a.f(-2)大于f(0)大于 2020-12-08 …