早教吧作业答案频道 -->数学-->
在矩形ABCD中,AB=4,BC=8,经过对角线交点O的直线EF绕点O旋转,分别交AD、BC于点E、F,连接AF、CE.(1)如图(1),依据下列条件在普通四边形、梯形、普通平行四边形、矩菱形或正方形中选
题目详情
在矩形ABCD中,AB=4,BC=8,经过对角线交点O的直线EF绕点O旋转,分别交AD、BC于点E、F,连接AF、CE.
(1)如图(1),依据下列条件在普通四边形、梯形、普通平行四边形、矩菱形或正方形中选择填空:旋转过程中四边形AFCE始终为___;
当点E为AD的中点时四边形AFCE为___;
当EF⊥AC时四边形AFCE为___;
(2)如图(1),当EF⊥AC时,求AF的长;
(3)如图(2),在(2)的基础上,若动点P从A点出发,沿A→F→B→A运动一周停止,速度为每秒5厘米;同时点Q从C点出发,沿C→D→E→C运动一周停止,速度为每秒4厘米,在P、Q运动过程中,第几秒时,四边形APCQ是平行四边形?
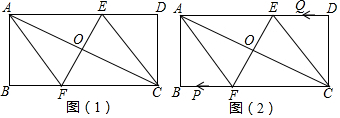
(1)如图(1),依据下列条件在普通四边形、梯形、普通平行四边形、矩菱形或正方形中选择填空:旋转过程中四边形AFCE始终为___;
当点E为AD的中点时四边形AFCE为___;
当EF⊥AC时四边形AFCE为___;
(2)如图(1),当EF⊥AC时,求AF的长;
(3)如图(2),在(2)的基础上,若动点P从A点出发,沿A→F→B→A运动一周停止,速度为每秒5厘米;同时点Q从C点出发,沿C→D→E→C运动一周停止,速度为每秒4厘米,在P、Q运动过程中,第几秒时,四边形APCQ是平行四边形?

▼优质解答
答案和解析
(1)当点E为AD的中点时,四边形AFCE为平行四边形;理由如下:
∵四边形ABCD是矩形,
∴AD∥BC,OA=OC,
∴∠CAD=∠ACB,∠AEF=∠CFE.
在△AOE和△COF中,
,
∴△AOE≌△COF(AAS),
∴AE=CF.
又∵AE∥CF,
∴四边形AFCE为平行四边形;
当点E为AD的中点时,AE=CF,AE∥CF,
则四边形AFCE为平行四边形;
当EF⊥AC时,四边形AFCE为菱形,理由如下:
∵由①知四边形AFCE为平行四边形,
∵EF⊥AC,
∴四边形AFCE为菱形;
故答案为:平行四边形;平行四边形;菱形.
(2) 设菱形的边长AF=CF=xcm,则BF=(8-x)cm,
在Rt△ABF中,AB=4cm,
由勾股定理得:AB2+BF2=AF2,
即42+(8-x)2=x2,
解得:x=5,
∴AF=5;
(3) 根据题意得,P点AF上时,Q点CD上,此时A,C,P,Q四点不可能构成平行四边形;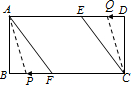
同理P点AB上时,Q点DE或CE上,也不能构成平行四边形.
∴只有当P点在BF上,Q点在ED上时,才能构成平行四边形,
∴以A,C,P,Q四点为顶点的四边形是平行四边形时,
PC=QA,
∵点P的速度为每秒5cm,点Q的速度为每秒4cm,运动时间为t秒,
∴PC=5t,QA=12-4t,
∴5t=12-4t,
解得:t=
,
∴以A,C,P,Q四点为顶点的四边形是平行四边形时,t=
秒.
∵四边形ABCD是矩形,
∴AD∥BC,OA=OC,
∴∠CAD=∠ACB,∠AEF=∠CFE.
在△AOE和△COF中,
|
∴△AOE≌△COF(AAS),
∴AE=CF.
又∵AE∥CF,
∴四边形AFCE为平行四边形;
当点E为AD的中点时,AE=CF,AE∥CF,
则四边形AFCE为平行四边形;
当EF⊥AC时,四边形AFCE为菱形,理由如下:
∵由①知四边形AFCE为平行四边形,
∵EF⊥AC,
∴四边形AFCE为菱形;
故答案为:平行四边形;平行四边形;菱形.
(2) 设菱形的边长AF=CF=xcm,则BF=(8-x)cm,
在Rt△ABF中,AB=4cm,
由勾股定理得:AB2+BF2=AF2,
即42+(8-x)2=x2,
解得:x=5,
∴AF=5;
(3) 根据题意得,P点AF上时,Q点CD上,此时A,C,P,Q四点不可能构成平行四边形;

同理P点AB上时,Q点DE或CE上,也不能构成平行四边形.
∴只有当P点在BF上,Q点在ED上时,才能构成平行四边形,
∴以A,C,P,Q四点为顶点的四边形是平行四边形时,
PC=QA,
∵点P的速度为每秒5cm,点Q的速度为每秒4cm,运动时间为t秒,
∴PC=5t,QA=12-4t,
∴5t=12-4t,
解得:t=
| 4 |
| 3 |
∴以A,C,P,Q四点为顶点的四边形是平行四边形时,t=
| 4 |
| 3 |
看了在矩形ABCD中,AB=4,B...的网友还看了以下:
如图,已知AC是矩形ABCD的对角线,过AC的中点O的直线EF,交BC于点F,交BC于点F,交AD 2020-04-09 …
初二几何正方形正方形ABCD的对角线交于O点,E是OA上任意一点,CF垂直于BE于F,CF交DB于 2020-05-13 …
如图所示,CD是Rt△ABC斜边AB上的高,AF为角平分线,AF交BC于F,交CD于E,过E作EG 2020-06-06 …
如图所示,CD是Rt△ABC斜边AB上的高,AF为角平分线,AF交BC于F,交CD于E,过E作EG 2020-06-23 …
如图所示,CD是Rt△ABC斜边AB上的高,AF为角平分线,AF交BC于F,交CD于E,过E作EG 2020-06-23 …
四边形ABCD为正方形,G是BC上任意一点,AE垂直与DG于点E,CF||AE交DG于点F 三角形 2020-06-27 …
1.已知菱形ABCD的两条对角线相交于点0,对角线AC=8cm,菱形的面积为16cm平方.求菱形的 2020-06-28 …
"地上交通"和"路面交通"两个词有什么区别书上说,城市综合交通从形式上可分为地上交通,路面交通,地 2020-06-29 …
四边形ABCD中,AB等于BC.BE垂直于AD垂足为E.角BCD减角ABE等于90度,过点C作CF 2020-07-13 …
如图,四边形ABCD是平行四边形,P是BD上任意一点,过P点的直线分别交AB,DC于E,F,交DA, 2020-12-25 …