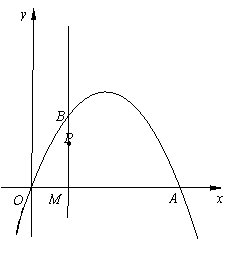
如图，已知二次函数的图像经过点B（12），与轴的另一个交点为A，点B关于抛物线对称轴的对称点为C，过点B作直线BM⊥轴垂足为点M．（1

Question

如图，已知二次函数 的图像经过点 B （ 1 2 ），与 轴的另一个交点为 A ，点 B 关于抛物线对称轴的对称点为 C ，过点 B 作直线 BM ⊥ 轴垂足为点 M ．

（ 1 ）求二次函数的解析式；

（ 2 ）在直线 BM 上有点 P （ 1 ， ），联结 CP 和 CA ，判断直线 CP 与直线 CA 的位置关系，并说明理由；

（ 3 ）在（ 2 ）的条件下，在坐标轴上是否存在点 E ，使得以 A 、 C 、 P 、 E 为

顶点的四边形为直角梯形，若存在，求出所有满足条件的点 E 的坐标；

若不存在，请说明理由。

Answer 1

答案： （ 1 ）∵点 B （ 1 2 ） 在 二次函数 的图像 上，

  ∴ -

∴二次函数的解析式为 -

（ 2 ） 直线 CP 与直线 CA 的位置关系是垂直

∵二次函数的解析式为

∴点 A (3 0)   C (2 2)

∵ P （ 1 ， ）

∴        

∴     ∴∠ PCA =90 °

即 CP ⊥ CA

(3)  假设在坐标轴上存在点 E ，使得以 A 、 C 、 P 、 E 为顶点的四边形为直角梯形，

∵∠ PCA =90 °

则 ①当点 E 在 轴上， PE // CA

∴ △ CBP ∽△ PME ， ∴ ， ∴ ， ∴ ---------------(2 分 )

②当点 E 在 轴上， PC // AE

∴ △ CBP ∽△ AOE ，   ∴ ， ∴ ， ∴ --------------(2 分 )

即 点 Q 的坐标 、 时，以 A 、 C 、 P 、 E 为顶点的四边形为直角梯形。