早教吧作业答案频道 -->数学-->
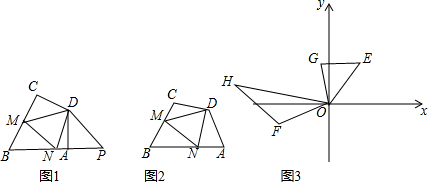
已知如图,在四边形ABCD中,AD=CD,M、N分别是BC、AB上的点.(1)如图①,若∠A=∠C=90°,∠B=∠MDN=60°.某同学在探究线段AN、MN、CM之间的数量关系时是这样的思路:延长BA到P,使AP=CM,
题目详情
已知如图,在四边形ABCD中,AD=CD,M、N分别是BC、AB上的点.
(1)如图①,若∠A=∠C=90°,∠B=∠MDN=60°.某同学在探究线段AN、MN、CM之间的数量关系时是这样的思路:延长BA到P,使AP=CM,连接PD(图1中虚线),通过研究图中有关三角形全等,再利用全等三角形的性质结合题中条件进行转化,从而得到结论.
这位同学在这个研究过程中:证明两对三角形分别全等的依据是___,得出线段AN、MN、CM之间的数量关系的结论是___.
(2)如图②,若∠A+∠C=180°,其他条件不变,当AN、MN、CM之间满足(1)中的数量关系时,设∠B=α°,请求出∠MDN的度数(用α含的代数式表示);
(3)如图③,我区某学校在庆祝“六一”儿童节的定向越野活动中,大本营指挥部设在点O处,甲同学在指挥部东北方向的E处,乙同学在指挥部南偏西75°的F处,且两位同学到指挥部的距离相等.接到行动指令后,甲同学以100米/分钟的速度向正西方向前进,乙同学以120米/分钟的速度向北偏西60°方向前进.10分钟后,指挥部监测到甲、乙两同学分别到达G、H处,且么∠GOH=75°,求此时甲、乙两同学之间的距离.
(1)如图①,若∠A=∠C=90°,∠B=∠MDN=60°.某同学在探究线段AN、MN、CM之间的数量关系时是这样的思路:延长BA到P,使AP=CM,连接PD(图1中虚线),通过研究图中有关三角形全等,再利用全等三角形的性质结合题中条件进行转化,从而得到结论.
这位同学在这个研究过程中:证明两对三角形分别全等的依据是___,得出线段AN、MN、CM之间的数量关系的结论是___.
(2)如图②,若∠A+∠C=180°,其他条件不变,当AN、MN、CM之间满足(1)中的数量关系时,设∠B=α°,请求出∠MDN的度数(用α含的代数式表示);
(3)如图③,我区某学校在庆祝“六一”儿童节的定向越野活动中,大本营指挥部设在点O处,甲同学在指挥部东北方向的E处,乙同学在指挥部南偏西75°的F处,且两位同学到指挥部的距离相等.接到行动指令后,甲同学以100米/分钟的速度向正西方向前进,乙同学以120米/分钟的速度向北偏西60°方向前进.10分钟后,指挥部监测到甲、乙两同学分别到达G、H处,且么∠GOH=75°,求此时甲、乙两同学之间的距离.

▼优质解答
答案和解析
(1)如图1,
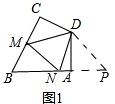
延长BA到P,使AP=CM,连接PD,
∵∠BAD=∠C=90°,
∴∠DAP=90°,
在△CDM和△ADP中
,
∴△CDM≌△ADP(SAS),
∴DM=DP,∠CDM=∠ADP,
在四边形ABCD中,∠C=∠BAD=90°,∠B=60°,
∴根据四边形的内角和得,∠ADC=120°,
∵∠MDN=60°,
∴∠CDM+∠ADN=60°,
∵∠CDM=∠ADP,
∴∠MDN=∠PDN,
在△DMN和△DPN中,
,
∴△DMN≌△DPN(SAS),
∴MN=PN=AN+AP=AN+CM;
故答案为:SAS,SAS,MN=AN+CM
(2)如图2,
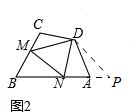
延长BA到P,使AP=CM,连接PD,
∵∠BAD+∠C=180°,∠BAD+∠DAP=180°,
∴∠C=∠DAP,
在△CDM和△ADP中
,
∴△CDM≌△ADP(SAS),
∴DM=DP,∠CDM=∠ADP,
∵CM=AP,
∴MN=AN+CM=AN+AP=PN,
在△DMN和△DPN中,
∴△DMN≌△DPN(SSS),
∴∠MDN=∠PDN=∠ADP+∠ADN,
∵∠CDM=∠ADP,
∴∠MDN=∠CDM+∠ADN=
∠ADC,
在四边形ABCD中,∠BAD+∠C=180°,
∴根据四边形的内角和得,∠B+∠ADC=180°,
∴∠B+2∠MDN=180°,
∵∠B=α,
∴∠MDN=
=90°-
α.
(3)如图3,
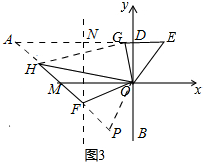
延长EG,FH相较于点A,过点F作FN⊥AE,
∴乙同学以120米/分钟的速度向北偏西60°方向前进,
∴∠NFA=60°,
∴∠A=30°,
∵甲同学在指挥部东北方向的E处,乙同学在指挥部南偏西75°的F处,
∴∠DOE=45°,∠BOF=75°,
∴∠MOF=90°-75°=15°,
∴∠EOF=∠DOE+∠DOM+MOF=150°,
∴∠A+∠EOF=180°,
延长AF至点P,使FP=GE,
满足(1)的条件,则有HG=HP=HF+FP,
∵甲同学以100米/分钟的速度向正西方向前进,乙同学以120米/分钟的速度向北偏西60°方向前进.10分钟后,指挥部监测到甲、乙两同学分别到达G、H处,
∴GE=100×10=1000米,HF=120×10=1200米,
∴HG=HF+FP=1200+1000=2200米,
即:甲、乙两同学之间的�

延长BA到P,使AP=CM,连接PD,
∵∠BAD=∠C=90°,
∴∠DAP=90°,
在△CDM和△ADP中
|
∴△CDM≌△ADP(SAS),
∴DM=DP,∠CDM=∠ADP,
在四边形ABCD中,∠C=∠BAD=90°,∠B=60°,
∴根据四边形的内角和得,∠ADC=120°,
∵∠MDN=60°,
∴∠CDM+∠ADN=60°,
∵∠CDM=∠ADP,
∴∠MDN=∠PDN,
在△DMN和△DPN中,
|
∴△DMN≌△DPN(SAS),
∴MN=PN=AN+AP=AN+CM;
故答案为:SAS,SAS,MN=AN+CM
(2)如图2,

延长BA到P,使AP=CM,连接PD,
∵∠BAD+∠C=180°,∠BAD+∠DAP=180°,
∴∠C=∠DAP,
在△CDM和△ADP中
|
∴△CDM≌△ADP(SAS),
∴DM=DP,∠CDM=∠ADP,
∵CM=AP,
∴MN=AN+CM=AN+AP=PN,
在△DMN和△DPN中,
|
∴△DMN≌△DPN(SSS),
∴∠MDN=∠PDN=∠ADP+∠ADN,
∵∠CDM=∠ADP,
∴∠MDN=∠CDM+∠ADN=
| 1 |
| 2 |
在四边形ABCD中,∠BAD+∠C=180°,
∴根据四边形的内角和得,∠B+∠ADC=180°,
∴∠B+2∠MDN=180°,
∵∠B=α,
∴∠MDN=
| 180°-α |
| 2 |
| 1 |
| 2 |
(3)如图3,

延长EG,FH相较于点A,过点F作FN⊥AE,
∴乙同学以120米/分钟的速度向北偏西60°方向前进,
∴∠NFA=60°,
∴∠A=30°,
∵甲同学在指挥部东北方向的E处,乙同学在指挥部南偏西75°的F处,
∴∠DOE=45°,∠BOF=75°,
∴∠MOF=90°-75°=15°,
∴∠EOF=∠DOE+∠DOM+MOF=150°,
∴∠A+∠EOF=180°,
延长AF至点P,使FP=GE,
满足(1)的条件,则有HG=HP=HF+FP,
∵甲同学以100米/分钟的速度向正西方向前进,乙同学以120米/分钟的速度向北偏西60°方向前进.10分钟后,指挥部监测到甲、乙两同学分别到达G、H处,
∴GE=100×10=1000米,HF=120×10=1200米,
∴HG=HF+FP=1200+1000=2200米,
即:甲、乙两同学之间的�
看了已知如图,在四边形ABCD中,...的网友还看了以下:
已知函数f(x)=3sin2x-2cos2x-1,x∈R.(Ⅰ)求函数f(x)的最小正周期和最小值 2020-04-27 …
已知曲线C的极坐标方程ρ=2,给定两点P(0,π/2),Q(-2,π),则有()A.P在曲线C上, 2020-05-15 …
已知极限limx→0x−arctanxxk=c,其中k,c为常数,且c≠0,则()A.k=2,c= 2020-06-12 …
已知圆C的方程为x2+y2+2x-6y-6=0,O为坐标原点.(Ⅰ)求过点M(-5,11)的圆C的 2020-06-14 …
(2002•荆门)阅读下列范例,按要求解答问题.例:已知实数a、b、c满足a+b+2c=1,a2+ 2020-07-20 …
如图,已知AE∥FC,∠A=∠C.(1)若∠1=60°,求∠2的度数.(2)试说明AD∥BC.(2 2020-07-29 …
已知:如图,∠B=∠C,∠1=∠3.求证:∠A=∠D.请把下面的推理过程填写完整.证明:∵∠B=∠ 2020-08-02 …
解答题(1)已知A=5x2+4x-1,B=-x2-3x+3,C=8-7x-6x2,求A-B+C的值. 2020-10-31 …
如图实线为某电场的电场线,虚线为等势线,已知c为线段ab的中点,过a、b的等势线的电势分别为30V和 2020-12-05 …
阅读下列范例,按要求解答问题.例:已知实数a、b、c满足a+b+2c=1,a2+b2+6c+32=0 2020-12-18 …