早教吧作业答案频道 -->数学-->
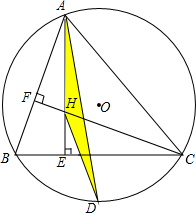
已知,△ABC内接于O,∠BAC=60°,AE⊥BC,CF⊥AB.AE,CF相交于点H,点D为弧BC的中点,连接HD,AD.求证:△AHD为等腰三角形.
题目详情
已知,△ABC内接于 O,∠BAC=60°,AE⊥BC,CF⊥AB.AE,CF相交于点H,点D为弧BC的中点,连接HD,AD.求证:△AHD为等腰三角形.

▼优质解答
答案和解析
证明:连接AO、OD,过O作OM⊥AC,则AM=
AC,如图所示: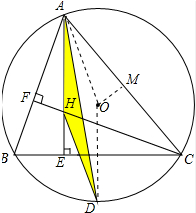
∵∠BAC=60°,CF⊥AB,
∴AF=
AC,
∴AM=AF,
∵AE⊥BC,CF⊥AB,
∴∠ABC+∠FHE=180°,
∵∠FHE+∠AHF=180°,
∴∠ABC=∠AHF,
∵∠AOM=
∠AOC=∠ABC,
∴∠AHF=∠AOM,
在△AMO与△AFH中,
,
∴△AMO≌△AFH(AAS),
∴AO=AH,
∵OD=OA,
∴AO=AH=OD,
∵点D为弧BC的中点,
∴OD⊥BC,
∵AE⊥BC,
∴AE∥OD,
∴四边形OAHD为平行四边形,
∵AO=AH,
∴四边形AHDO是菱形,
∴AH=HD,
∴△AHD为等腰三角形.
| 1 |
| 2 |

∵∠BAC=60°,CF⊥AB,
∴AF=
| 1 |
| 2 |
∴AM=AF,
∵AE⊥BC,CF⊥AB,
∴∠ABC+∠FHE=180°,
∵∠FHE+∠AHF=180°,
∴∠ABC=∠AHF,
∵∠AOM=
| 1 |
| 2 |
∴∠AHF=∠AOM,
在△AMO与△AFH中,
|
∴△AMO≌△AFH(AAS),
∴AO=AH,
∵OD=OA,
∴AO=AH=OD,
∵点D为弧BC的中点,
∴OD⊥BC,
∵AE⊥BC,
∴AE∥OD,
∴四边形OAHD为平行四边形,
∵AO=AH,
∴四边形AHDO是菱形,
∴AH=HD,
∴△AHD为等腰三角形.
看了已知,△ABC内接于O,∠BA...的网友还看了以下:
如图物体A、B、C叠放在水平桌面上,水平力F作用于C物体,使A、B、C以共同速度向右匀速运动,关于 2020-05-13 …
〖诗词出处及作者〗A.不是花中偏爱菊,此花开尽更无花B.更无柳絮因风起,唯有葵花向日倾C.清香传得 2020-05-15 …
下列命题正确的是()A.若函数f(x)在x=a处连续,则函数f(x)在x=a的邻域内连续B.若函数 2020-06-12 …
已知可导函数f(x)的导函数为g(x),且满足:①g(x)-1x-1>0;②f(2-x)-f(x) 2020-06-18 …
设f(x)=|x(1-x)|,则()A.x=0是f(x)的极值点,但(0,0)不是曲线y=f(x) 2020-06-30 …
下列说法正确的是()A.石油是混合物,汽油是纯净物B.沸点:汽油>煤油>柴油>润滑油C.分馏汽油� 2020-07-05 …
F=A+A×(1+i)+…+A×(1+i)n-1,(1)等式两边同乘以(1+i):F(1+i)=A( 2020-11-01 …
下列说法不正确的是()A.声、光和电磁波都能传递信息B.微波炉是利用电磁波来加热食品的C.固定电话、 2020-11-03 …
已知f(x)=(1/2)x,a,b∈R+,A=f(A+B)/2,G=f根号ab...则AGH的大小关 2020-11-03 …
A.早期猿人B.晚期猿人C.早期智人D.晚期智人1.中国山顶洞人2.德国尼安德特人3.印尼爪哇人4. 2020-11-06 …