已知函数y=f（x）是定义域为R的偶函数．当x≥0时，f（x）=54sin(π2x)(0≤x≤1)(14)x+1(x>1)，若关于x的方程5[f（x）]2-（5a+6）f（x）+6a=0（a∈R），有且仅有6个不同实数根，则实数a的取值范围是（

Question

已知函数y=f（x）是定义域为R的偶函数．当x≥0时，f（x）=

(5)/(4)sin((π)/(2)x)(0≤x≤1)

((1)/(4))x+1(x>1)

，若关于x的方程5[f（x）]²-（5a+6）f（x）+6a=0（a∈R），有且仅有6个不同实数根，则实数a的取值范围是（　　）

A. 0<a<1或a=

(5)/(4)

B. 0≤a≤1或a=

(5)/(4)

C. 0<a≤1或a=

(5)/(4)

D. 1<a≤

(5)/(4)或a=0

Answer 1

函数y=f（x）是定义域为R的偶函数，
当x≥0时，f（x）=

(5)/(4)sin((π)/(2)x)(0≤x≤1)

((1)/(4))x+1(x>1)

，
当x<0时，f（x）=

-(5)/(4)sin((π)/(2)x)，-1≤x≤0

4x+1，x<-1

．
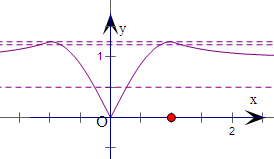
作出函数f（x）的图象如右．
由于关于x的方程5[f（x）]²-（5a+6）f（x）+6a=0，
解得f（x）=a或f（x）=(6)/(5)，
当0≤x≤1时，f（x）∈[0，(5)/(4)]，x>1时，f（x）∈（1，(5)/(4)）．
由1<(6)/(5)<(5)/(4)，则f（x）=(6)/(5)有4个实根，
由题意，只要f（x）=a有2个实根，
则由图象可得当0<a≤1时，f（x）=a有2个实根，
当a=(5)/(4)时，f（x）=a有2个实根．
综上可得：0<a≤1或a=(5)/(4)．
故选：C．