早教吧作业答案频道 -->数学-->
在平面直角坐标系中,点A、B分别在x轴、y轴上,点A与点C关于y轴对称,点E是线段AC上的点(点E不与点A、C重合)(1)若点A的坐标为(a,0),则点C的坐标为;(2)如图1,点F是线段AB上
题目详情
在平面直角坐标系中,点A、B分别在x轴、y轴上,点A与点C关于y轴对称,点E是线段AC上的点(点E不与点A、C重合)
(1)若点A的坐标为(a,0),则点C的坐标为___;
(2)如图1,点F是线段AB上的点,若∠BEF=∠BAO,∠BAO=2∠OBE,求证:AF=CE;
(3)如图2,若点D为AC上一点,连接ED,满足BE=BD,试探究∠ABE与∠DEC的关系.
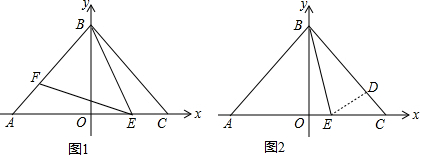
(1)若点A的坐标为(a,0),则点C的坐标为___;
(2)如图1,点F是线段AB上的点,若∠BEF=∠BAO,∠BAO=2∠OBE,求证:AF=CE;
(3)如图2,若点D为AC上一点,连接ED,满足BE=BD,试探究∠ABE与∠DEC的关系.

▼优质解答
答案和解析
(1)∵点A(a,0)与点C关于y轴对称,
∴C(-a,0),
故答案为(-a,0).,
(2)设∠OBE=α,
∴∠BAO=2∠OBE=2α,∠BEF=∠BAO=α,
由对称得,OA=OC,
∵BO⊥AC,
∴AB=CB,
∴∠BAO=∠BCO=2α,
∴∠ABE=∠ABO+∠OBE=90°-α,
在△BEF中,∠BFE=180°-(∠BEF+∠EBF)=90°-α,
∴∠ABE=∠BFE,
∴BE=EF,
在Rt△AOB中,∠ABO=90°-2α,
∴∠ACB=2α,∠CBO=∠90°-2α,
∵∠OBE=α,
∴∠CBE=90°-3α,
在△BCE中,根据三角形的内角和得,∠BEC=90°+α,
∴∠AEF=180°-∠BEF-∠BEC=90°-3α,
∴∠CBE=∠AEF,
在△AEF和△CBE中,
,
∴△AEF≌△CBE,
∴AF=CE,
(3)设∠OBE=α,∠CBE=β,
∴∠CBO=α+β,由(1)知,∠ABO=∠CBO=α+β,
∴∠ABE=∠ABO+∠OBE=α+β+α=2α+β,
在Rt△OBE中,∠OEB=90°-α,
在△BDE中,BD=BE,
∴∠BED=90°-
β,
∴∠DEC=180°-∠OEB-∠BED=
(2α+β),
∵∠ABE=2α+β,
∴∠ABE=2∠DEC.
∴C(-a,0),
故答案为(-a,0).,
(2)设∠OBE=α,
∴∠BAO=2∠OBE=2α,∠BEF=∠BAO=α,
由对称得,OA=OC,
∵BO⊥AC,
∴AB=CB,
∴∠BAO=∠BCO=2α,
∴∠ABE=∠ABO+∠OBE=90°-α,
在△BEF中,∠BFE=180°-(∠BEF+∠EBF)=90°-α,
∴∠ABE=∠BFE,
∴BE=EF,
在Rt△AOB中,∠ABO=90°-2α,
∴∠ACB=2α,∠CBO=∠90°-2α,
∵∠OBE=α,
∴∠CBE=90°-3α,
在△BCE中,根据三角形的内角和得,∠BEC=90°+α,
∴∠AEF=180°-∠BEF-∠BEC=90°-3α,
∴∠CBE=∠AEF,
在△AEF和△CBE中,
|
∴△AEF≌△CBE,
∴AF=CE,
(3)设∠OBE=α,∠CBE=β,
∴∠CBO=α+β,由(1)知,∠ABO=∠CBO=α+β,
∴∠ABE=∠ABO+∠OBE=α+β+α=2α+β,
在Rt△OBE中,∠OEB=90°-α,
在△BDE中,BD=BE,
∴∠BED=90°-
| 1 |
| 2 |
∴∠DEC=180°-∠OEB-∠BED=
| 1 |
| 2 |
∵∠ABE=2α+β,
∴∠ABE=2∠DEC.
看了在平面直角坐标系中,点A、B分...的网友还看了以下:
若点P不在角平分线上,如图,如何过点P画直线与角的两边相交组成等腰三角形,能画出几个,要求给图 2020-05-13 …
关于质点系动量守恒定律A:质点系不受外力作用,且无非保守力时,动量守恒。B:质点系所受的合外力的冲 2020-05-17 …
若外力对质点系不做功,则该质点系的() A.动量一定守恒 B.动能一定守恒 C.机械能一定守恒 D 2020-06-06 …
已知在矩形ABCD中,AB=2,BC=3,P是线段AD边上的任意一点(不含端点A、D),连接PC, 2020-06-06 …
(1)如图(一),P是∠AOB平分线上一点,试过点P画一条直线,交角的两边于点C、D,使△OCD是 2020-06-08 …
已知等边△abc,它的高为h如图(1)若点p在△abc内,则点p到△abc的三边的距离和h的大小关 2020-06-12 …
(1)在同一个平面直角坐标系中,若点的位置不变,则点的坐标;若点的位置改变,则点的坐标.(2)建立 2020-07-01 …
如图,△ABC为等边三角形,点P是边AC的延长线上一点,连接BP,作∠BPQ等于60°,直线PQ与 2020-07-24 …
质点系不受外力作用或所受外力的矢量和为零时,质点系的()为一常矢量A、角动量B、机械能C、动量D、 2020-08-03 …
关于质点系动量守恒定律,说法正确的是:A、质点系不受外力作用,且无非保守内力时,动量守恒.B、质点系 2020-12-22 …