早教吧作业答案频道 -->数学-->
两个形状大小完全一样的两个Rt△ACB和Rt△DCE如图放置,设两直角边BC、CE的夹角∠ECB=α,∠A=β.(1)求证:EM=BN;(2)当α、β满足什么关系时,△AMC是等腰三角形.
题目详情
两个形状大小完全一样的两个Rt△ACB和Rt△DCE如图放置,设两直角边BC、CE的夹角∠ECB=α,∠A=β.
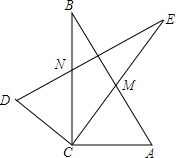
(1)求证:EM=BN;
(2)当α、β满足什么关系时,△AMC是等腰三角形.

(1)求证:EM=BN;
(2)当α、β满足什么关系时,△AMC是等腰三角形.
▼优质解答
答案和解析
(1)证明:∵Rt△ACB≌Rt△DCE,
∴AC=CD,∠A=∠D,CB=CE,
∵∠ACB=∠DCE=90°,
∴∠DCN=∠ACM,
在△DCN与△ACM中,
,
∴△DCN≌△ACM,
∴CN=CM,
∴CB-CN=CE-CM,
即EM=BN;
(2)∵∠BCE=α,
∴∠ACM=90°-α,
∴①当∠MCA=∠A,即90°-α=β时,△ACM是等腰三角形,
∴当α+β=90°时,△ACM是等腰三角形,
②当∠CMA=∠A,即90°-α+2β=180°时,△ACM是等腰三角形,
∴2β-α=90°时,△ACM是等腰三角形,
③当∠MCA=∠AMC,即2(90°-α)+β=180时,△ACM是等腰三角形,
∴β=2α时,△ACM是等腰三角形.
∴AC=CD,∠A=∠D,CB=CE,
∵∠ACB=∠DCE=90°,
∴∠DCN=∠ACM,
在△DCN与△ACM中,
|
∴△DCN≌△ACM,
∴CN=CM,
∴CB-CN=CE-CM,
即EM=BN;
(2)∵∠BCE=α,
∴∠ACM=90°-α,
∴①当∠MCA=∠A,即90°-α=β时,△ACM是等腰三角形,
∴当α+β=90°时,△ACM是等腰三角形,
②当∠CMA=∠A,即90°-α+2β=180°时,△ACM是等腰三角形,
∴2β-α=90°时,△ACM是等腰三角形,
③当∠MCA=∠AMC,即2(90°-α)+β=180时,△ACM是等腰三角形,
∴β=2α时,△ACM是等腰三角形.
看了 两个形状大小完全一样的两个R...的网友还看了以下:
足球以8m/s的速度飞来,运动员在0.2s的时间内将足球以12m/s的速度反向踢出.足球在这段时间 2020-06-04 …
(2014•北京)对某一个函数给出如下定义:若存在实数M>0,对于任意的函数值y,都满足-M≤y≤ 2020-06-23 …
若函数y=f(x)满足f(-x)=f(x),当a,b∈(-∞,0]时总有f(a)−f(b)a−b> 2020-06-27 …
如图所示,物块A的质量为M,物块B、C的质量都是m.且m<M<2m.三物块用细线通过轻质滑轮连接, 2020-07-13 …
昨天卖出48个足球,今天比昨天多卖出m个,今天卖出足球个.当m=10时,今天卖出个.当m=时,今天 2020-07-17 …
已知a>b>0,全集U=R,集合M={x|b<x<a+b2},N={x|ab<x<a},P={x| 2020-07-30 …
对某一个函数给出如下定义:若存在实数M>0,对于任意的函数值y,都满足-M≤y≤M,则称这个函数是 2020-07-31 …
设非空集合M、N满足:M={x|f(x)=0},N={x|g(x)=0},P={x|f(x)g(x 2020-08-01 …
已知函数f(x)=x3-x2,x∈R.(Ⅰ)若正数m、n满足m•n>1,证明:f(m)、f(n)至少 2020-11-19 …
如果有理数m,n满足|m|-n=0,那么m,n的关系是()A.互为相反数B.m=±n且n≥0C.相等 2021-02-02 …