某公园内直线道路旁有一半径为10米的半圆形荒地（圆心O在道路上，AB为直径），现要在荒地的基础上改造出一处景观．在半圆上取一点C，道路上B点的右边取一点D，使OC垂直于CD，且OD的长

Question

某公园内直线道路旁有一半径为10米的半圆形荒地（圆心O在道路上，AB为直径），现要在荒地的基础上改造出一处景观．在半圆上取一点C，道路上B点的右边取一点D，使OC垂直于CD，且OD的长不超过20米．在扇形区域AOC内种植花卉，三角形区域OCD内铺设草皮．已知种植花卉的费用每平方米为200元，铺设草皮的费用每平方米为100元．

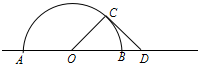
（1）设∠COD=x（单位：弧度），将总费用y表示为x的函数式，并指出x的取值范围；
（2）当x为何值时，总费用最低？并求出最低费用．

Answer 1

（1）因为扇形AOC的半径为10 m，∠AOC=π-x（rad），
所以扇形AOC的面积为
S扇AOC=((π-x)•102)/(2)=50(π-x)，0<x≤(π)/(3)；…（3分）
在Rt△COD中，OC=10，CD=10tanx，
所以△COD的面积为
S_△COD=(1)/(2)•OC•CD=50tanx；…（5分）
所以y=100S_△COD+200S_扇形AOC=5000（tanx+2π-2x），0<x≤(π)/(3)；…（8分）
（注：没有x的范围，扣1分）
（2）设f(x)=tanx+2π-2x，0<x≤(π)/(3)，
则f(x)=(sinx)/(cosx)+2π-2x，
f′(x)=(cos2x+sin2x)/(cos2x)-2=(1-2cos2x)/(cos2x)，
令f'（x）=0，解得x=(π)/(4)，…（11分）
从而当0<x<(π)/(4)时，f'（x）<0；
当(π)/(4)<x<(π)/(3)，f′（x）>0；
因此f（x）在区间(0，(π)/(4))上单调递减；在区间((π)/(4)，(π)/(3))上单调递增；
当x=(π)/(4)时，f（x）取得最小值，
且f((π)/(4))=1+2π-(π)/(2)=1+(3π)/(2)；…（14分）
所以y的最小值为（5000+7500π）元； …（15分）
答：当x=(π)/(4)时，改造景观的费用最低，最低费用为（5000+7500π）元．     …（16分）