早教吧作业答案频道 -->数学-->
已知椭圆在椭圆上.(1)求椭圆的离心率;(2)设A为椭圆的左顶点,O为坐标原点.若点Q在椭圆上且满足AQ=AO,求直线OQ的斜率的值.
题目详情
已知椭圆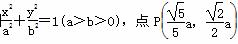 在椭圆上.
在椭圆上.
(1) 求椭圆的离心率;
(2) 设A为椭圆的左顶点,O为坐标原点.若点Q在椭圆上且满足AQ=AO,求直线OQ的斜率的值.
▼优质解答
答案和解析
(2) 设直线OQ的斜率为k,则其方程为y=kx,设点Q的坐标为(x0,y0). 由条件得消去y0并整理得x=.① 由AQ=AO,A(-a,0)及y0=kx0,得(x0+a)2+k2x=a2. 整理得(1+k2)x+2ax0=0,而x0≠0,故x0=,代入①,整理得(1+k2)2=4k2·+4. 由(1)知=,故(1+k2)2=k2+4, 即5k4-22k2-15=0,可得k2=5.所以直线OQ的斜率k=±.
看了 已知椭圆在椭圆上.(1)求椭...的网友还看了以下:
如图,圆心O的半径为5,点P为圆心O外一点,OP=8,以点P为圆心做半径为R的圆(1)当圆心P与圆 2020-05-23 …
最好稍微写下原因.不然看不懂.RT△ABC中,∠C=90°,AC=5,BC=12,以点C为圆心r为 2020-06-06 …
数学圆问题1.在rt△ABC中,∠C=90°,AC=12,BC=5,以点A为圆心做圆A,要使B,C 2020-06-09 …
已知椭圆的左焦点F为圆的圆心,且椭圆上的点到点F的距离最小值为。(I)求椭圆方程;(II)已知经过 2020-07-20 …
在平面直角坐标系xOy中,圆M:(x-a)2+(y+a-3)2=1(a>0),点N为圆M上任意一点 2020-07-20 …
在平面直角坐标系中点A的坐标为(40)一点A为圆心4为半径的圆与x轴交于OB两点P是x轴的一个动点 2020-07-26 …
在Rt△ABC中,∠ACB=90°,AC=6,AB=10,以点C为圆心作圆,设圆的半径为r(1)要 2020-07-26 …
如图,圆O是以直l上一点O为圆心,半径为1的圆,sin角AOB=1/3,点P在直线l上运动,若过点 2020-07-26 …
在平面直角坐标系xoy中,圆M:(x-a)2+(y+a-3)2=1(a>0),点N为圆M上任意一点 2020-07-26 …
在平面直角坐标系xOy中,已知点A(t,0),B(t+2,0),M(3,4).以点M为圆心,1为半 2020-08-03 …