早教吧作业答案频道 -->数学-->
己知矩形ABCD,P为矩形所在平面内的任意一点,求证:PA2+PC2=PB2+PD2.(提示:应分P在矩形内、P在矩形上、P在矩形外,三种情形加以讨论.)
题目详情
己知矩形ABCD,P为矩形所在平面内的任意一点,求证:PA2+PC2=PB2+PD2.(提示:应分P在矩形内、P在矩形上、P在矩形外,三种情形加以讨论.)
▼优质解答
答案和解析
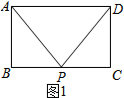 证明:①如图1,P在矩形的边上,
证明:①如图1,P在矩形的边上,
在Rt△ABP中,由勾股定理,得PA2-PB2=AB2,
同理可得PD2-PC2=CD2,
由矩形的性质可得AB=CD,
∴PA2-PB2=PD2-PC2,
∴PA2+PC2=PB2+PD2.
②P在矩形内,如图2,过点P作AD的垂线,交AD于点E,交BC于点F,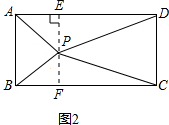
则四边形ABFE和CDEF为矩形,
∴AE=BF,DE=CF,
由勾股定理得:
则AP2=AE2+PE2,PC2=PF2+CF2,
BP2=BF2+PF2,PD2=DE2+PE2,
∴PA2+PC2=AE2+PE2+PF2+CF2,
PB2+PD2=BF2+PF2+DE2+PE2,
∴PA2+PC2=PB2+PD2.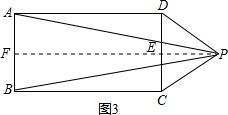
③P在矩形外,如图3,过P作PF⊥AB于F,交CD于E,
则PE⊥CD,
∴四边形AFED与四边形BCEF是矩形,
∴BF=CE,AF=DE,
由勾股定理得:
则AP2=AF2+PF2,PC2=PE2+CE2,
BP2=BF2+PF2,PD2=DE2+PE2,
∴PA2+PC2=AF2+PF2+PE2+CE2,
PB2+PD2=BF2+PF2+DE2+PE2,
∴PA2+PC2=PB2+PD2.
 证明:①如图1,P在矩形的边上,
证明:①如图1,P在矩形的边上,在Rt△ABP中,由勾股定理,得PA2-PB2=AB2,
同理可得PD2-PC2=CD2,
由矩形的性质可得AB=CD,
∴PA2-PB2=PD2-PC2,
∴PA2+PC2=PB2+PD2.
②P在矩形内,如图2,过点P作AD的垂线,交AD于点E,交BC于点F,

则四边形ABFE和CDEF为矩形,
∴AE=BF,DE=CF,
由勾股定理得:
则AP2=AE2+PE2,PC2=PF2+CF2,
BP2=BF2+PF2,PD2=DE2+PE2,
∴PA2+PC2=AE2+PE2+PF2+CF2,
PB2+PD2=BF2+PF2+DE2+PE2,
∴PA2+PC2=PB2+PD2.

③P在矩形外,如图3,过P作PF⊥AB于F,交CD于E,
则PE⊥CD,
∴四边形AFED与四边形BCEF是矩形,
∴BF=CE,AF=DE,
由勾股定理得:
则AP2=AF2+PF2,PC2=PE2+CE2,
BP2=BF2+PF2,PD2=DE2+PE2,
∴PA2+PC2=AF2+PF2+PE2+CE2,
PB2+PD2=BF2+PF2+DE2+PE2,
∴PA2+PC2=PB2+PD2.
看了己知矩形ABCD,P为矩形所在...的网友还看了以下:
已知一个三角形有一个内接正方形,正方形的边长是60/37,当这个三方形有一个由两已知一个三角形有一 2020-05-17 …
角,等腰三角形,等边三角形,平行四边形,矩形,菱形,正方形,等腰梯形,正五边形,圆等图形中,是轴对 2020-06-04 …
(2013•武汉)已知四边形ABCD中,E,F分别是AB,AD边上的点,DE与CF交于点G.(1) 2020-06-18 …
(1998•江西)矩形、菱形、正方形都是平行四边形,但它们都是有特殊条件的平行四边形.正方形不仅是 2020-07-30 …
解线性方程组讨论我想问下解线性方程组是不是一定要化成阶梯形矩阵?(主要想问下最后行一定要是零行吗比 2020-08-02 …
一根长13米的铁丝分成两段,做成一个矩形和一个正方形,已知矩形的长和宽之比为2:1,矩形的长比正方形 2020-11-10 …
下列说法中,正确的是()A.对角线互相垂直的四边形是菱形B.对角线相等的四边形是矩形C.四条边相等的 2020-12-25 …
面积是2500的矩形、三角形、菱形各有几个?边长是整数,面积是2500的矩形、三角形、菱形各有几个? 2020-12-25 …
长方形,正方形与矩形有什么区别需要非常细致专业解答而且,有人说正方形是特殊的矩形,还有人说正方形是特 2021-01-04 …
1.对角线相等的四边形是矩形.2.三角形不是多边形.3.对角线互相垂直且有一组邻边相等的四边形是菱形 2021-02-01 …