早教吧作业答案频道 -->数学-->
如图,在直角坐标系中,Rt△ABC位于第一象限,两条直角边AC、AB分别平行于x轴、y轴,点A的坐标为(1,1),AB=2,AC=3.(1)求BC边所在直线的解析式;(2)若反比例函数y=mx(x>0)的图象经
题目详情
如图,在直角坐标系中,Rt△ABC位于第一象限,两条直角边AC、AB分别平行于x轴、y轴,点A的坐标为(1,1),AB=2,AC=3.
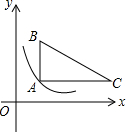
(1)求BC边所在直线的解析式;
(2)若反比例函数y=
(x>0)的图象经过点A,求m的值;
(3)若反比例函数y=
(x>0)的图象与△ABC有公共点,请直接写出n的取值范围.

(1)求BC边所在直线的解析式;
(2)若反比例函数y=
| m |
| x |
(3)若反比例函数y=
| n |
| x |
▼优质解答
答案和解析
(1)∵Rt△ABC位于第一象限,两条直角边AC、AB分别平行于x轴、y轴,点A的坐标为(1,1),AB=2,AC=3,
∴B(1,3),C(4,1),
设直线BC的解析式为y=kx+b(k≠0),
∴
,解得
,
∴BC边所在直线的解析式为:y=-
x+
;
(2)∵反比例函数y=
(x>0)的图象经过点A(1,1),
∴m=1;
(3)∵反比例函数y=
的图象与△ABC有公共点,
∴当函数经过A(1,1)时,n=1;
当函数图象经过点C(4,1)时,n=4,
当反比例函数与线段BC相切时,设y=
过BC上一点(a,-
a+
),
则n=a(-
a+
)=-
(a-
)2+
,
∴n最大=
.
∴1≤n≤
.
∴B(1,3),C(4,1),
设直线BC的解析式为y=kx+b(k≠0),
∴
|
|
∴BC边所在直线的解析式为:y=-
| 2 |
| 3 |
| 11 |
| 3 |
(2)∵反比例函数y=
| m |
| x |
∴m=1;
(3)∵反比例函数y=
| n |
| x |
∴当函数经过A(1,1)时,n=1;
当函数图象经过点C(4,1)时,n=4,
当反比例函数与线段BC相切时,设y=
| n |
| x |
| 2 |
| 3 |
| 11 |
| 3 |
则n=a(-
| 2 |
| 3 |
| 11 |
| 3 |
| 2 |
| 3 |
| 11 |
| 4 |
| 121 |
| 24 |
∴n最大=
| 121 |
| 24 |
∴1≤n≤
| 121 |
| 24 |
看了如图,在直角坐标系中,Rt△A...的网友还看了以下:
直线AB:y=-x-b分别与x、y轴交于A (6,0)、B两点,过点B的直线交x轴负半轴于C,且O 2020-05-17 …
如图所示,点A1,A2,A3在x轴上,且OA1=A1A2=A2A3,分别过点A1,A2,A3作y轴 2020-05-21 …
直线Y=-4\3X+6分别于X轴Y轴交于AB两点直线Y=4/5x于AB教育点C于过点A且平行于Y轴 2020-06-15 …
直线Y=-4\3X+6分别于X轴Y轴教育AB两点直线Y=4/5x于AB教育点C于过点A切平行于Y轴 2020-06-15 …
如图:直线y=-x+18分别与x轴、y轴交于A、B两点;直线y=2x分别与AB交于C点,与过点A且 2020-07-20 …
对数函数关于各直线对称的关系式请说明对数函数关于Y轴,X轴,原点,Y=X,Y=-X对称的关系式!如 2020-07-30 …
在坐标平面中,直线y=x+5分别交x轴、y轴于A、B,直线y=-2x+20分别交x轴、y轴于C、D 2020-07-30 …
在空间直角坐标系中的点P(a,b,c),有下列叙述:①点P(a,b,c)关于横轴(x轴)的对称点是 2020-07-30 …
如图,直线y=二分之一x+1分别与x轴、y轴交于点A、B直线y=x+b分别与x轴、y轴交于点C、D直 2020-11-01 …
直线y=-四分之三x+6与x轴、y轴分别交于AB两点,直线y=五分之四x与AB交于C与过A平行于y轴 2020-12-13 …