早教吧作业答案频道 -->数学-->
如图,己知AB是O的直径,且AB=4,点C在半径OA上(点C与点O、点A不重合),过点C作AB的垂线交O于点D.连接OD,过点B作OD的平行线交O于点E,交CD的延长线于点F.(1)若点E是BD的中点,求∠F
题目详情
如图,己知AB是 O的直径,且AB=4,点C在半径OA上(点C与点O、点A不重合),过点C作AB的垂线交 O于点D.连接OD,过点B作OD的平行线交 O于点E,交CD的延长线于点F.
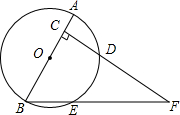
(1)若点E是
的中点,求∠F的度数;
(2)求证:BE=2OC;
(3)设AC=x,则当x为何值时BE•EF的值最大?最大值是多少?

(1)若点E是
 |
| BD |
(2)求证:BE=2OC;
(3)设AC=x,则当x为何值时BE•EF的值最大?最大值是多少?
▼优质解答
答案和解析
(1)如图1,连接OE.
∵
=
,
∴∠BOE=∠EOD,
∵OD∥BF,
∴∠DOE=∠BEO,
∵OB=OE,
∴∠OBE=∠OEB,
∴∠OBE=∠OEB=∠BOE=60°,
∵CF⊥AB,
∴∠FCB=90°,
∴∠F=30°;
(2)连接OE,过O作OM⊥BE于M,
∵OB=OE,
∴BE=2BM,
∵OD∥BF,
∴∠COD=∠B,
在△OBM与△ODC中
,
∴△OBM≌△ODC,
∴BM=OC,
∴BE=2OC;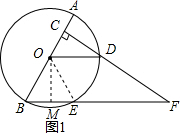
(3)∵OD∥BF,
∴△COD∽△CBF,
∴
=
,
∵AC=x,AB=4,
∴OA=OB=OD=2,
∴OC=2-x,BE=2OC=4-2x,
∴
=
,
∴BF=
,
∴EF=BF-BE=
,
∴BE•EF=
•2(2-x)=-4x2+12x=-4(x-
)2+9,
∴当x=
时,最大值=9.
∵
 |
| ED |
 |
| BE |
∴∠BOE=∠EOD,
∵OD∥BF,
∴∠DOE=∠BEO,
∵OB=OE,
∴∠OBE=∠OEB,
∴∠OBE=∠OEB=∠BOE=60°,
∵CF⊥AB,
∴∠FCB=90°,
∴∠F=30°;
(2)连接OE,过O作OM⊥BE于M,
∵OB=OE,
∴BE=2BM,
∵OD∥BF,
∴∠COD=∠B,
在△OBM与△ODC中
|
∴△OBM≌△ODC,
∴BM=OC,
∴BE=2OC;

(3)∵OD∥BF,
∴△COD∽△CBF,
∴
| OC |
| BC |
| OD |
| BF |
∵AC=x,AB=4,
∴OA=OB=OD=2,
∴OC=2-x,BE=2OC=4-2x,
∴
| 2-x |
| 4-x |
| 2 |
| BF |
∴BF=
| 8-2x |
| 2-x |
∴EF=BF-BE=
| -2x2+6x |
| 2-x |
∴BE•EF=
| -2x2+6x |
| 2-x |
| 3 |
| 2 |
∴当x=
| 3 |
| 2 |
看了如图,己知AB是O的直径,且A...的网友还看了以下:
在平行四边形ABCD中,点E,F分别是线段AD,BC上的两动点,点E从点A向D运动在平行四边形AB 2020-05-13 …
在等腰三角形△ABC(C为顶点)中,CH是底边上的高线,点P是线段CH上不与端点重和的任意一点,连 2020-06-05 …
快开学了,1)将平行四边形ABCD的对角线交点与直角坐标系的原点重合,且点A,B的坐标分别为(-2 2020-07-04 …
如图△ABC中,AB=AC=10厘米,BC=12厘米,D是BC的中点,点P从B出发,以a厘米/秒( 2020-07-14 …
如图,在Rt△ABC中,∠B=90°,BC=53,∠C=30°.点D从点C出发沿CA方向以每秒2个 2020-07-17 …
设正整数n≥2,对2×n格点链中的2n个结点用红(R)、黄(Y)、蓝(B)三种颜色染色,左右端点中 2020-07-20 …
如图所示,O为两个等量异号点电荷连线中点,P为连线中垂线上的任意一点,分别用U0、UP、E0、EP 2020-07-30 …
(2009海南)如图,两等量异号的点电荷相距为2a.M与两点电荷共线,N位于两点电荷连线的中垂线上 2020-07-30 …
已知点A是圆F1:(x+3)2+y2=16上任意一点,点F2与点F1关于原点对称.线段AF2的中垂 2020-08-01 …
如图,在Rt△ABC中,∠B=90°,∠C=30°,AC=48,点D从点C出发沿CA方向以每秒4个 2020-08-03 …