定义:如果一个与的函数图象经过平移后能与某反比例函数的图象重合,那么称这个函数是与的“反比例平移函数”.例如:的图象向左平移2
定义:如果一个 ![]() 与
与 ![]() 的函数图象经过平移后能与某反比例函数的图象重合,那么称这个函数是
的函数图象经过平移后能与某反比例函数的图象重合,那么称这个函数是 ![]() 与
与 ![]() 的“反比例平移函数”.
的“反比例平移函数”.
例如 : ![]() 的图象向左平移 2 个单位,再向下平移 1 个单位得到
的图象向左平移 2 个单位,再向下平移 1 个单位得到 ![]() 的图象,则
的图象,则 ![]() 是
是 ![]() 与
与 ![]() 的“反比例平移函数”.
的“反比例平移函数”.
( 1 ) 若矩形的两边分别是 2 ![]() 、 3
、 3 ![]() ,当这两边分别增加
,当这两边分别增加 ![]() (
( ![]() ) 、
) 、 ![]() (
( ![]() ) 后,得到的新矩形的面积为 8
) 后,得到的新矩形的面积为 8 ![]() ,求
,求 ![]() 与
与 ![]() 的函数表达式,并判断这个函数是否为“反比例平移函数”.
的函数表达式,并判断这个函数是否为“反比例平移函数”.
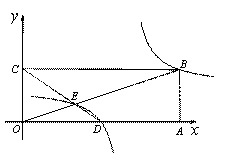
( 2 )如图,在平面直角坐标系中,点 ![]() 为原点,矩形
为原点,矩形 ![]() 的顶点
的顶点 ![]() 、
、 ![]() 的坐标分别为 (9 , 0) 、 (0 , 3) .点
的坐标分别为 (9 , 0) 、 (0 , 3) .点 ![]() 是
是 ![]() 的中点,连接
的中点,连接 ![]() 、
、 ![]() 交于点
交于点 ![]() ,“反比例平移函数”
,“反比例平移函数” ![]() 的图象经过
的图象经过 ![]() 、
、 ![]() 两点.则这个“反比例平移函数”的表达式为 ;这个“反比例平移函数”的图象经过适当的变换与某一个反比例函数的图象重合,请写出这个反比例函数的表达式 .
两点.则这个“反比例平移函数”的表达式为 ;这个“反比例平移函数”的图象经过适当的变换与某一个反比例函数的图象重合,请写出这个反比例函数的表达式 .
( ![]() 3 )在( 2 )的条件下, 已知过线段
3 )在( 2 )的条件下, 已知过线段 ![]() 中点的一条直线
中点的一条直线 ![]() 交这个“反
交这个“反
比例平移函数”图象于 ![]() 、
、 ![]() 两点 (
两点 ( ![]() 在
在 ![]() 的右侧 ) , 若
的右侧 ) , 若 ![]() 、
、 ![]() 、
、
![]() 、
、 ![]() 为顶点组成的四边形面积为 16 ,请求出点
为顶点组成的四边形面积为 16 ,请求出点 ![]() 的坐标.
的坐标.
( 1 ) ![]() ,
,
∴ ![]()
![]() 向右平移 2 个单位,再向上平移 3 个单位得到
向右平移 2 个单位,再向上平移 3 个单位得到 ![]() . ∴
. ∴ ![]() 是 “反比例平移函数” . ……2 分
是 “反比例平移函数” . ……2 分
( 2 ) “反比例平移函数”的表达式为 ![]() .
.
变换后的反比例函数表达式为 ![]() .
.
( 3 ) 如图, 当点 ![]() 在点
在点 ![]() 左侧时, 设线段
左侧时, 设线段 ![]() 的中点为
的中点为 ![]() ,由反比
,由反比
例函数中心对称性,四边形 ![]() 为平行四边形 .
为平行四边形 .
∵四边形 ![]() 的面积为 16 ,∴
的面积为 16 ,∴ ![]() =4 ,
=4 ,
∵ ![]() (9 3) ,
(9 3) , ![]() (6 2).
(6 2).
![]() 是
是 ![]() 的 “反比例平移函数”,
的 “反比例平移函数”,
∴ ![]() =
= ![]() =4 ,
=4 , ![]()
![]() (3 1)
(3 1)
过 ![]() 作
作 ![]() 轴的垂线,与
轴的垂线,与 ![]() 、
、 ![]() 轴分别交于
轴分别交于 ![]() 、
、 ![]() 点 .
点 .
![]() .
.
设 ![]() ,
,
∴ 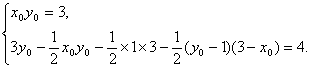
即 
∴ 
∴ ![]() (1 , 3) , ∴点
(1 , 3) , ∴点 ![]() 的坐标为( 7 , 5 ) .
的坐标为( 7 , 5 ) .
当点 ![]() 在点
在点 ![]() 右侧时, 同理可得 点
右侧时, 同理可得 点 ![]() 的坐标为( 15 ,
的坐标为( 15 , ![]() ) .
) .

![]()
如图所示,坐标平面第1象限内存在大小为、方向水平向左的匀强电场,在第II象限内存在方向垂直纸面向里 2020-05-14 …
定义:如果一个与的函数图象经过平移后能与某反比例函数的图象重合,那么称这个函数是与的“反比例平移函 2020-05-14 …
如图所示,在竖直空间建立直角坐标系xOy,在第一象限和第四象限内存在竖直向上的,电场强度大小为E1 2020-05-17 …
如图所示,坐标平面第1象限内存在大小为E=3×105N/C、方向水平向左的匀强电场,在第II象限内 2020-07-18 …
如图所示xOy坐标系,在第二象限内有水平向右的匀强电场,在第一、第四象限内分别存在匀强磁场,磁感应 2020-07-19 …
(2012•茂名一模)如图所示,坐标平面第Ⅰ象限内存在大小为E=4×105N/C方向水平向左的匀强 2020-07-31 …
(17分)如图所示,在xoy平面直角坐标系的第一象限有射线OA,OA与x轴正方向夹角为30°,OA 2020-07-31 …
如图所示,直角坐标系XOY位于竖直平面内,在竖直的Y轴右侧存在垂直XOY平面向里的匀强磁场,磁感应 2020-08-03 …
(2013•临汾三模)在竖直平面内建立一平面直角坐标系xoy,x轴沿水平方向,如图甲所示.第二象限内 2020-12-18 …
如图所示,在第Ⅱ象限内有水平向右的匀强电场,在第Ⅰ象限和第Ⅳ象限的圆形区域内分别存在如图所示的匀强磁 2021-01-08 …