早教吧作业答案频道 -->数学-->
已知,点P是直角三角形ABC斜边AB上一动点(不与A,B重合),分别过点A,B向直线CP作垂线,垂足分别为E,F,Q为斜边AB的中点.(1)当点P与点Q重合时,如图1,写出QE与QF的数量关系,不证明
题目详情
已知,点P是直角三角形ABC斜边AB上一动点(不与A,B重合),分别过点A,B向直线CP作垂线,垂足分别为E,F,Q为斜边AB的中点.
(1)当点P与点Q重合时,如图1,写出QE与QF的数量关系,不证明;
(2)当点P在线段AB上且不与点Q重合时,如图2,(1)的结论是否成立?并证明;
(3)当点P在线段BA(或AB)的延长线上时,如图3,此时(1)的结论是否成立?请画出图形并给予证明.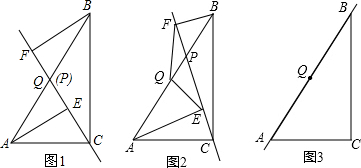
(1)当点P与点Q重合时,如图1,写出QE与QF的数量关系,不证明;
(2)当点P在线段AB上且不与点Q重合时,如图2,(1)的结论是否成立?并证明;
(3)当点P在线段BA(或AB)的延长线上时,如图3,此时(1)的结论是否成立?请画出图形并给予证明.

▼优质解答
答案和解析
 (1)QE=QF,
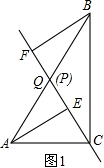
(1)QE=QF,
理由是:如图1,∵Q为AB中点,
∴AQ=BQ,
∵BF⊥CP,AE⊥CP,
∴∠BFQ=∠AEQ=90°,
在△BFQ和△AEQ中
∴△BFQ≌△AEQ(AAS),
∴QE=QF,
(2)(1)中的结论仍然成立,
证明:如图2,延长FQ交AE于D,
∵Q为AB中点,
∴AQ=BQ,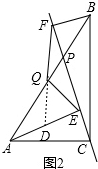
∵BF⊥CP,AE⊥CP,
∴BF∥AE,
∴∠QAD=∠FBQ,
在△FBQ和△DAQ中,
,
∴△FBQ≌△DAQ(ASA),
∴QF=QD,
∵AE⊥CP,
∴EQ是Rt△DEF斜边上的中线,
∴QE=QF=QD,
即QE=QF.
(3)(1)中的结论仍然成立,
证明:如图3,
延长EQ、FB交于D,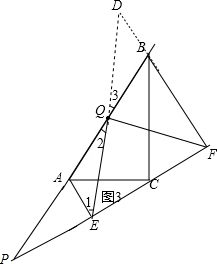
∵Q为AB中点,
∴AQ=BQ,
∵BF⊥CP,AE⊥CP,
∴BF∥AE,
∴∠1=∠D,
在△AQE和△BQD中,
,
∴△AQE≌△BQD(AAS),
∴QE=QD,
∵BF⊥CP,
∴FQ是Rt△DEF斜边DE上的中线,
∴QE=QF.
 (1)QE=QF,
(1)QE=QF,理由是:如图1,∵Q为AB中点,
∴AQ=BQ,
∵BF⊥CP,AE⊥CP,
∴∠BFQ=∠AEQ=90°,
在△BFQ和△AEQ中
|
∴△BFQ≌△AEQ(AAS),
∴QE=QF,
(2)(1)中的结论仍然成立,
证明:如图2,延长FQ交AE于D,
∵Q为AB中点,
∴AQ=BQ,

∵BF⊥CP,AE⊥CP,
∴BF∥AE,
∴∠QAD=∠FBQ,
在△FBQ和△DAQ中,
|
∴△FBQ≌△DAQ(ASA),
∴QF=QD,
∵AE⊥CP,
∴EQ是Rt△DEF斜边上的中线,
∴QE=QF=QD,
即QE=QF.
(3)(1)中的结论仍然成立,
证明:如图3,
延长EQ、FB交于D,

∵Q为AB中点,
∴AQ=BQ,
∵BF⊥CP,AE⊥CP,
∴BF∥AE,
∴∠1=∠D,
在△AQE和△BQD中,
|
∴△AQE≌△BQD(AAS),
∴QE=QD,
∵BF⊥CP,
∴FQ是Rt△DEF斜边DE上的中线,
∴QE=QF.
看了已知,点P是直角三角形ABC斜...的网友还看了以下:
已知a,b,c为△ABC的三边,且(a-c):(a+b):(c-b)=-2:7:1已知a,b,c为△ 2020-03-31 …
1.一个多边形的每个外角都相等,如果它的内角与外角的度数之比是13:2,求这个多边形的边数.2.已 2020-04-26 …
在△ABC中,a,b,c为∠A,∠B,∠C的对边,已知a=2倍根号3,b=6,∠A=30°在△AB 2020-05-13 …
圆o的半径为r,其内接正三角形,正方形,正六边形的边长为a,b,c(1)求a,b,c的值(2)以a 2020-06-03 …
1.已知a,b,c为△ABC的边,且满足a²(c²-a²)=b²(c²-b²),试判断此三角形的形 2020-06-05 …
设|a|=4,|b|=3,向量a,b夹角是30度,求以a+2b和a-3b为边的平行四边形的面积是? 2020-06-06 …
一道关于勾股定理的小题直角三角形的两条直角边分别为a、b,斜边为c,斜边上的高为h,则以c+h,a 2020-06-10 …
若a,b,c为△ABC的三边,且(x+a)(x+b)+(x+b)(x+c)+(x+c)(x+a)为 2020-06-12 …
已知a,b,c为三角形的三边,且满足a^2+b^2+c^2=ab+bc+ac已知a,b,c为三角形 2020-07-15 …
已知a,b,c为△ABC的三边且满足a²(b-c)+b²(c-a)+c²(a-b)=0,试判断△A 2020-07-17 …