早教吧作业答案频道 -->数学-->
设f(x)=ex-a(x+1).(1)若a>0,f(x)≥0对一切x∈R恒成立,求a的最大值;(2)设是曲线y=g(x)上任意两点,若对任意的a≤-1,直线AB的斜率恒大于常数m,求m的取值范围;(3)
题目详情
设f(x)=e x -a(x+1).
(1)若a>0,f(x)≥0对一切x∈R恒成立,求a的最大值;
(2)设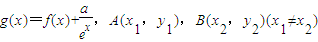 是曲线y=g(x)上任意两点,若对任意的a≤-1,直线AB的斜率恒大于常数m,求m的取值范围;
是曲线y=g(x)上任意两点,若对任意的a≤-1,直线AB的斜率恒大于常数m,求m的取值范围;
(3)是否存在正整数a.使得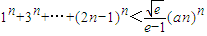 对一切正整数n都成立?若存在,求a的最小值;若不存在,请说明理由.
对一切正整数n都成立?若存在,求a的最小值;若不存在,请说明理由.
(1)若a>0,f(x)≥0对一切x∈R恒成立,求a的最大值;
(2)设
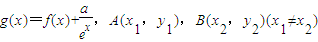 是曲线y=g(x)上任意两点,若对任意的a≤-1,直线AB的斜率恒大于常数m,求m的取值范围;
是曲线y=g(x)上任意两点,若对任意的a≤-1,直线AB的斜率恒大于常数m,求m的取值范围;(3)是否存在正整数a.使得
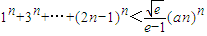 对一切正整数n都成立?若存在,求a的最小值;若不存在,请说明理由.
对一切正整数n都成立?若存在,求a的最小值;若不存在,请说明理由.▼优质解答
答案和解析
分析:
(1)由f(x)=ex-a(x+1),知f′(x)=ex-a,故f(x)min=f(lna)=a-a(lna+1)=-alna,再由f(x)≥0对一切x∈R恒成立,能amax.(2)由f(x)=ex-a(x+1),知g(x)=f(x)+=.由a≤-1,直线AB的斜率恒大于常数m,知g′(x)=ex--a≥2-a=-a+2=m,(a≤-1),由此能求出实数m的取值范围.(3)设t(x)=ex-x-1,则t′(x)=ex-1,从而得到ex≥x+1,取,用累加法得到.由此能够推导出存在正整数a=2.使得1n+3n+…+(2n-1)n<?(an)n.
(1)∵f(x)=ex-a(x+1),∴f′(x)=ex-a,∵a>0,f′(x)=ex-a=0的解为x=lna.∴f(x)min=f(lna)=a-a(lna+1)=-alna,∵f(x)≥0对一切x∈R恒成立,∴-alna≥0,∴alna≤0,∴amax=1.(2)∵f(x)=ex-a(x+1),∴g(x)=f(x)+=.∵a≤-1,直线AB的斜率恒大于常数m,∴g′(x)=ex--a≥2-a=-a+2=m,(a≤-1),解得m≤3,∴实数m的取值范围是(-∞,3].(3)设t(x)=ex-x-1,则t′(x)=ex-1,令t′(x)=0得:x=0.在x<0时t′(x)<0,f(x)递减;在x>0时t′(x)>0,f(x)递增.∴t(x)最小值为f(0)=0,故ex≥x+1,取,得,累加得.∴1n+3n+…+(2n-1)n<?(2n)n,故存在正整数a=2.使得1n+3n+…+(2n-1)n<?(an)n.
点评:
本题考查满足条件的实数的最大值的求法,考查满足条件地实数的取值范围的求法,探索满足条件的实数的最小值.综合性强,难度大.解题时要认真审题,合理地运算导数性质进行等价转化.
分析:
(1)由f(x)=ex-a(x+1),知f′(x)=ex-a,故f(x)min=f(lna)=a-a(lna+1)=-alna,再由f(x)≥0对一切x∈R恒成立,能amax.(2)由f(x)=ex-a(x+1),知g(x)=f(x)+=.由a≤-1,直线AB的斜率恒大于常数m,知g′(x)=ex--a≥2-a=-a+2=m,(a≤-1),由此能求出实数m的取值范围.(3)设t(x)=ex-x-1,则t′(x)=ex-1,从而得到ex≥x+1,取,用累加法得到.由此能够推导出存在正整数a=2.使得1n+3n+…+(2n-1)n<?(an)n.
(1)∵f(x)=ex-a(x+1),∴f′(x)=ex-a,∵a>0,f′(x)=ex-a=0的解为x=lna.∴f(x)min=f(lna)=a-a(lna+1)=-alna,∵f(x)≥0对一切x∈R恒成立,∴-alna≥0,∴alna≤0,∴amax=1.(2)∵f(x)=ex-a(x+1),∴g(x)=f(x)+=.∵a≤-1,直线AB的斜率恒大于常数m,∴g′(x)=ex--a≥2-a=-a+2=m,(a≤-1),解得m≤3,∴实数m的取值范围是(-∞,3].(3)设t(x)=ex-x-1,则t′(x)=ex-1,令t′(x)=0得:x=0.在x<0时t′(x)<0,f(x)递减;在x>0时t′(x)>0,f(x)递增.∴t(x)最小值为f(0)=0,故ex≥x+1,取,得,累加得.∴1n+3n+…+(2n-1)n<?(2n)n,故存在正整数a=2.使得1n+3n+…+(2n-1)n<?(an)n.
点评:
本题考查满足条件的实数的最大值的求法,考查满足条件地实数的取值范围的求法,探索满足条件的实数的最小值.综合性强,难度大.解题时要认真审题,合理地运算导数性质进行等价转化.
看了 设f(x)=ex-a(x+1...的网友还看了以下:
已知P(-1,1),Q(2,2)过原点且斜率存在的直线L恒与线段PQ相交,求直线L的倾斜角a取值范 2020-04-11 …
有一个物体是三角体长2.7宽1.67高有两个面是斜的两个面是直的求体积公式怎么列? 2020-04-11 …
问一道物理题..高一的,关于船渡河的.问一道物理题..北风速度4m/s,大河中的水流正以3m/s的 2020-04-13 …
过定点A(m,0)(m0)于P、Q两点,又Q关于x轴对称点为Q1,连接PQ1交x轴于B点。(1)求 2020-05-02 …
汽车质量为m=2×10^3kg,沿平直的路面以恒定功率20kw由静止出发,经过60s,汽车达到最大 2020-05-13 …
直线恒在曲线的上方.已知曲线C:y=1/3x^3-x^2-4x+1,直线l:x+y+2k-1=0, 2020-05-14 …
椭圆方程X2/2+Y2=1,有一条直线过(0,-1/3)交椭圆于A,B两点.求证;以AB为直径的圆 2020-05-15 …
..椭圆C:x2/4+ y2=1 M(0,-1) 直线l:y=kx+m与椭圆C相交与不同的两点A、 2020-05-16 …
高中数学--圆的直线方程已知圆C:x^2+(y-1)^2=5,直线l:mx-y+1-m=0问:设直 2020-05-16 …
直线与圆2(918:23:13)圆C:(x-1)2+(y-2)2=25,直线L:(2m+1)x+( 2020-05-17 …