早教吧作业答案频道 -->数学-->
设函数f(x)=(2x-1)ex-ax+a,若存在唯一的整数x0使得f(x0)<0,则实数a的取值范围是.
题目详情
设函数f(x)=(2x-1)ex-ax+a,若存在唯一的整数x0使得f(x0)<0,则实数a的取值范围是___.
▼优质解答
答案和解析
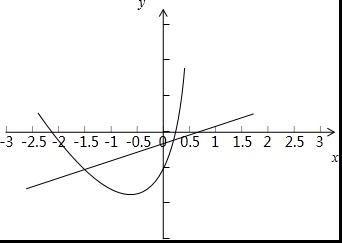 令g(x)=(2x-1)ex,h(x)=a(x-1),
令g(x)=(2x-1)ex,h(x)=a(x-1),
∵g'(x)=(2x-1)ex+2ex=(2x+1)ex,
∴当x<-
时,g'(x)<0,则函数g(x)在(-∞,-
)上单调递减;
当x>-
时,g'(x)>0,则函数g(x)在(-
,+∞)上单调递增;
而g(-1)=-3e-1,g(0)=-1;
因为存在唯一的整数x0使得f(x0)<0.
即(2x0-1)ex<a(x0-1).
所以结合图形知:
即:
,解得
≤a<1;
故答案为:[
,1).
 令g(x)=(2x-1)ex,h(x)=a(x-1),
令g(x)=(2x-1)ex,h(x)=a(x-1),∵g'(x)=(2x-1)ex+2ex=(2x+1)ex,
∴当x<-
| 1 |
| 2 |
| 1 |
| 2 |
当x>-
| 1 |
| 2 |
| 1 |
| 2 |
而g(-1)=-3e-1,g(0)=-1;
因为存在唯一的整数x0使得f(x0)<0.
即(2x0-1)ex<a(x0-1).
所以结合图形知:
|
即:
|
| 3 |
| 2e |
故答案为:[
| 3 |
| 2e |
看了 设函数f(x)=(2x-1)...的网友还看了以下:
已知函数f(x)=2a+1/a-1/a2x,常数a>0.1.设m.n>0,证明:函数f(x)在[已 2020-05-16 …
设a>0,f(x)=e^x/a+a/e^x是R上的偶函数,求a值.∵f(x)=e^x/a+a/e^ 2020-05-17 …
设f(x)=ax²+bx+c(a,b,c∈R,a≠0)f(x)在区间[-2,2]上的最大值最小值分 2020-06-02 …
设a>0,f(x)=(e^x/a)+(a/e^x)在R上的图像关于y轴对称;求:①求a的值.②求证 2020-06-03 …
一道大学导数题设F(x)=g(x)f(x),f(x)在x=a处连续,但不可导,又g'(a)存在,则 2020-07-15 …
设f(x)是定义在R上的单调增函数,证明集合{x|对任意a>0,f(x+a)>f(x-a)}设f( 2020-07-29 …
概率密度函数的计算题设X的概率密度有关系:f(-x)=f(x),证明任意a>0,F(-a)=1-F 2020-07-30 …
已知三次函数f(x)=ax3+bx2+cx+d(a≠0),设f'(x)是函数y=f(x)的导数,f 2020-07-31 …
数学题!大家帮忙哦!xEa设a>0,f(X)=---+---,且f(-x)=f(x)函数,axE1 2020-07-31 …
一道函数题设A是由26个英文字母组成的集合,设B={0,1,2,...,24,25}对应法则f为f 2020-08-02 …