早教吧作业答案频道 -->数学-->
如图所示,l1,l2是互相垂直的异面直线,MN是它们的公垂线段,点A,B在直线l1上,且位于M点的两侧,C在l2上,AM=BM=NM=CN(1)求证:异面直线AC与BN垂直;(2)若四面体ABCN的体积VABCN=9,求异
题目详情
如图所示,l1,l2是互相垂直的异面直线,MN是它们的公垂线段,点A,B在直线l1上,且位于M点的两侧,C在l2上,AM=BM=NM=CN
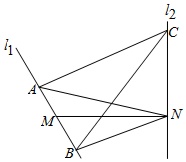
(1)求证:异面直线AC与BN垂直;
(2)若四面体ABCN的体积VABCN=9,求异面直线l1,l2之间的距离.

(1)求证:异面直线AC与BN垂直;
(2)若四面体ABCN的体积VABCN=9,求异面直线l1,l2之间的距离.
▼优质解答
答案和解析
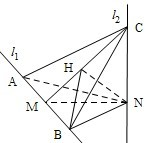 (1)证明:由已知l2⊥MN,l2⊥l1,MN∩l1=M,可得l2⊥平面ABN.
(1)证明:由已知l2⊥MN,l2⊥l1,MN∩l1=M,可得l2⊥平面ABN.
由已知MN⊥l1,AM=MB=MN,
可知AN=NB且AN⊥NB.
又AN为AC在平面ABN内的射影.
∴AC⊥NB
(2)∵AM=BM=NM=CN,MN是它们的公垂线段,
就是异面直线l1,l2之间的距离,
由中垂线的性质可得AN=BN,四面体ABCN的体积VABCN=9,
可得:VABCN=9=
×
AB×MN×CN=
MN3,
∴MN=3.
异面直线l1,l2之间的距离为3.
 (1)证明:由已知l2⊥MN,l2⊥l1,MN∩l1=M,可得l2⊥平面ABN.
(1)证明:由已知l2⊥MN,l2⊥l1,MN∩l1=M,可得l2⊥平面ABN.由已知MN⊥l1,AM=MB=MN,
可知AN=NB且AN⊥NB.
又AN为AC在平面ABN内的射影.
∴AC⊥NB
(2)∵AM=BM=NM=CN,MN是它们的公垂线段,
就是异面直线l1,l2之间的距离,
由中垂线的性质可得AN=BN,四面体ABCN的体积VABCN=9,
可得:VABCN=9=
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
∴MN=3.
异面直线l1,l2之间的距离为3.
看了 如图所示,l1,l2是互相垂...的网友还看了以下:
在矩形ABCD中,AB=根号三,AD=根号六,M是BC的中线,联接AM,BD,求证:AM垂直BD 2020-05-17 …
如图1,Rt△ABC中AB=AC,点D、E是线段AC上两动点,且AD=EC,AM垂直BD,垂足为M 2020-06-13 …
如图,直线l1l2垂直,垂足为点O,AM⊥l1,AN⊥l2,垂足分别为M,N,AM=4,AN=3如 2020-07-20 …
如图1,Rt△ABC中AB=AC,点D、E是线段AC上两动点,且AD=EC,AM垂直BD,垂足为M 2020-07-30 …
已知椭圆x24+y2=1的左顶点为A,过A作两条互相垂直的弦AM、AN交椭圆于M、N两点.(1)当 2020-07-31 …
如图,⊙O1与⊙O2相交于A、B两点,过点B的直线交⊙O1、⊙O2于C、D,BD的中点为M,AM交⊙ 2020-10-30 …
(2006•临沂)如图1,已知正方形ABCD的对角线AC、BD相交于点O,E是AC上一点,连接EB, 2020-11-13 …
AD垂直AB,AD等于AB,AE垂直AC,AE等于AC,M为BC上一点,MA垂直DE于点F,且2AM 2020-12-05 …
在△ABC中,∠C=90°,AC=BC.过点C在△ABC外作直线MN,AM⊥MN于M,BN⊥MN于N 2020-12-09 …
已知等边三角形abc中,点o是边ac,bc垂直平分线的交点,m,n分别在直线ac,bc上,且角mon 2021-01-02 …