早教吧作业答案频道 -->数学-->
在△ABC和△DEC中,AC=BC,DC=EC,∠ACB=∠ECD=90°(1)如图1,当点A、C、D在同一条直线上时,求证:AF⊥BD;(2)如图2,当点A、C、D不在同一条直线上时,求证:AF⊥BD;(3)如图3,在(2)
题目详情
在△ABC和△DEC中,AC=BC,DC=EC,∠ACB=∠ECD=90°
(1)如图1,当点A、C、D在同一条直线上时,求证:AF⊥BD;
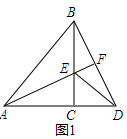
(2)如图2,当点A、C、D不在同一条直线上时,求证:AF⊥BD;
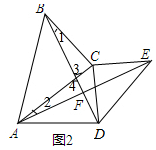
(3)如图3,在(2)的条件下,连接CF并延长CF交AD于点G,∠AFG是一个固定的值吗?若是,求出∠AFG的度数;若不是,请说明理由.
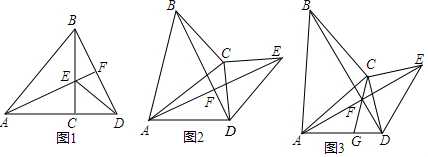
(1)如图1,当点A、C、D在同一条直线上时,求证:AF⊥BD;
(2)如图2,当点A、C、D不在同一条直线上时,求证:AF⊥BD;
(3)如图3,在(2)的条件下,连接CF并延长CF交AD于点G,∠AFG是一个固定的值吗?若是,求出∠AFG的度数;若不是,请说明理由.

▼优质解答
答案和解析
(1)证明:如图1中,
在△ACE和△BCD中,
,
∴△ACE≌△BCD,
∴∠EAC=∠∠CBD,∵∠AEC=∠BEF,
∴∠BFE=∠ACE=90°,
∴AF⊥BD.
(2)证明:如图2中,
∵∠ACB=∠ECD=90°,
∴∠ACB+∠ACD=∠ECD+∠ACD,
∴∠BCD=∠ACE,
在△ACE和△BCD中,
,
∴△ACE≌△BCD,
∴∠1=∠2,
∵∠3=∠4,
∴∠BFA=∠BCA=90°,
∴AF⊥BD.
(3)∠AFG=45°,
如图3,过点C作CM⊥BD,CN⊥AE,垂足分别为M、N,
∵△ACE≌△BCD,
∴S△ACE=S△BCD,AE=BD,
∴
•AE•CN=
•BD•CM,
∴CM=CN,∵CM⊥BD,CN⊥AE,
∴CF平分∠BFE,
∵AF⊥BD,
∴∠BFE=90°,
∴∠EFC=45°,
∴∠AFG=45°.

在△ACE和△BCD中,
|
∴△ACE≌△BCD,
∴∠EAC=∠∠CBD,∵∠AEC=∠BEF,
∴∠BFE=∠ACE=90°,
∴AF⊥BD.
(2)证明:如图2中,

∵∠ACB=∠ECD=90°,
∴∠ACB+∠ACD=∠ECD+∠ACD,
∴∠BCD=∠ACE,
在△ACE和△BCD中,
|
∴△ACE≌△BCD,
∴∠1=∠2,
∵∠3=∠4,
∴∠BFA=∠BCA=90°,
∴AF⊥BD.
(3)∠AFG=45°,
如图3,过点C作CM⊥BD,CN⊥AE,垂足分别为M、N,

∵△ACE≌△BCD,
∴S△ACE=S△BCD,AE=BD,
∴
| 1 |
| 2 |
| 1 |
| 2 |
∴CM=CN,∵CM⊥BD,CN⊥AE,
∴CF平分∠BFE,
∵AF⊥BD,
∴∠BFE=90°,
∴∠EFC=45°,
∴∠AFG=45°.
看了 在△ABC和△DEC中,AC...的网友还看了以下:
直线方程的五种形式已知直线1aX-bY+4=0和直线2(a-1)X+Y+b=0,当直线1和直线2平 2020-05-17 …
SOS(用斜率和直线方程求)一、求适合下列条件的直线方程1、经过点P(3,2),且在两坐标轴上的截 2020-05-21 …
已知直线y=-x+2与直线y=2/3x+2交于点c直线y=-x+2与x轴的交点为A直线y=2/3x 2020-05-23 …
设A是任意实数,则方程x^2*cosA+y^2=1所表示的曲线不可能是A.直线B双曲线C椭圆设A是 2020-06-02 …
初中数学,在直角坐标系中,直线L:Y=,-2x+4分别交x轴点A,直线Y=X与直线L交于点B初中数 2020-06-06 …
根据下列语句画出图形1.直线l与直线m相交于点A,直线m与直线n相交于点C,直线你与直线l相交于点 2020-06-12 …
在平面直角坐标系中直线y=x+1和y=-¾x+3交于点A,直线y=x+1交x轴于点B,直线y=-¾ 2020-06-14 …
1.判断把线段的2端无限延长,可以得到一条直线()三个角都是锐角的三角形叫做锐角三角形()同一平面 2020-07-04 …
在直角坐标系中,若一点的纵横坐标都是整数,则称该点为整点,设过点A(-2√2,-1+√2),B(0 2020-07-05 …
在平面直角坐标系中,坐标原点为O,直线1:y=x+4与x轴交于点A,直线2:y=-x+2与Y轴交于B 2020-11-01 …