已知各项均为正数的数列{an}满足：a1＝1，an+1·an＋an+1－an＝0(1)证明数列为等差数列，并求an；(2)设bn＝an·an+2，数列{bn}的前n项和为Sn，求证：．
已知各项均为正数的数列{a n }满足：a 1 ＝1，a n+1 ·a n ＋a n+1 －a n ＝0
(1)证明数列
为等差数列，并求a n ；
(2)设b n ＝a n ·a n+2 ，数列{b n }的前n项和为S n ，求证：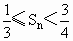
．
解析：
(1)证明：∵，且数列各项均为正数， ∴(常数) ∴数列为等差数列，首项，公差， ∴，∴ (2)∵，∴ ∴ ∵，∴， ∵函数在上是增函数，∴， 综上所述
⒈运算规定:(a*b)=|a-b| a,b为实数,求(√7*3)+√7 ⒉设⒈运算规定:(a*b) 2020-05-13 …
设a∈R,函数f(x)=a×2^x+a-2/2^x+1是奇函数,求a的值设a∈R,函数f(x)=a 2020-05-13 …
设数列｛a｝的前n项和为Sn,已知a1=a,an+1=Sn+3n次方设数列an的前n项和为Sn,已 2020-05-17 …
在关系数据库设计中,设计关系模式的任务属于()A. 需求设计B. 概念设计C. 逻辑设计D. 物理设 2020-05-23 …
应用系统设计包括______和数据库设计。A.数据设计B.软件平台设计C.硬件平台设计D.网络结构设 2020-05-24 …
设函数f(x)=√x^2+1.—ax,其中a>0,求a的取值范围,使函数f(x)在区间[0,+∞) 2020-06-20 …
一次函数,1.f（x)=2x+a,f(1)=4,求a的值2.设y=f(x)为一次函数,已知f(2) 2020-07-09 …
数学,线性代数,设A是方阵,A的k次方=0,k为正整数,求I+A+(A^2)/2!+(A^3)/.. 2020-11-20 …
已知直线l过点P(-3,2),且与x轴负半轴,y轴的正半轴分别交于A,B两点,设直线在x轴,y轴上的 2020-12-31 …
设函数f(x)=in(x2-ax+2）的定义域为A.⑴若2∈A,-2∈A（不属于A）,求实数a的范围 2021-01-31 …