早教吧作业答案频道 -->数学-->
如图,四边形ABCD内接于O,AC平分∠BAD,延长DC交AB的延长线于点E.(1)若∠ADC=86°,求∠CBE的度数;(2)若AC=EC,求证:AD=BE.
题目详情
如图,四边形ABCD内接于 O,AC平分∠BAD,延长DC交AB的延长线于点E.
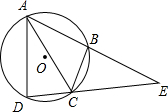
(1)若∠ADC=86°,求∠CBE的度数;
(2)若AC=EC,求证:AD=BE.

(1)若∠ADC=86°,求∠CBE的度数;
(2)若AC=EC,求证:AD=BE.
▼优质解答
答案和解析
(1) ∵四边形ABCD内接于 O,
∴∠ADC+∠ABC=180°,
又∵∠ADC=86°,
∴∠ABC=94°,
∴∠CBE=180°-94°=86°;
(2)证明:∵AC=EC,
∴∠E=∠CAE,
∵AC平分∠BAD,
∴∠DAC=∠CAB,
∴∠DAC=∠E,
∵四边形ABCD内接于 O,
∴∠ADC+∠ABC=180°,
又∵∠CBE+∠ABC=180°,
∴∠ADC=∠CBE,
在△ADC和△EBC中,
,
∴△ADC≌△EBC,
∴AD=BE.
∴∠ADC+∠ABC=180°,
又∵∠ADC=86°,
∴∠ABC=94°,
∴∠CBE=180°-94°=86°;
(2)证明:∵AC=EC,
∴∠E=∠CAE,
∵AC平分∠BAD,
∴∠DAC=∠CAB,
∴∠DAC=∠E,
∵四边形ABCD内接于 O,
∴∠ADC+∠ABC=180°,
又∵∠CBE+∠ABC=180°,
∴∠ADC=∠CBE,
在△ADC和△EBC中,
|
∴△ADC≌△EBC,
∴AD=BE.
看了 如图,四边形ABCD内接于O...的网友还看了以下:
圆锥曲线的已知椭圆C:x^2/2+y^2=1的右焦点为F,右准线为l,点A属于l,线段AF交C于点 2020-04-08 …
1.a·2^(-t/30)求导答案a·2(-t/30)·(-1/30)·ln22.已知函数f(x) 2020-05-23 …
1.椭圆C:x^2/a^2+y^2/b^2=1(a>b>0)两个焦点为F1、F2,点P在椭圆C上, 2020-06-03 …
已知圆C:x^2+y^2+ax-4y+1=0(a属于R),过定点P(0,1)作斜率为1的直线交圆C 2020-06-09 …
已知圆C:x^2+y^2+ax-4y+1=0(a属于R),过定点P(0,1)作斜率为1的直线交圆C 2020-06-09 …
已知圆C:x^2+y^2+ax-4y+1=0(a属于R),过定点P(0,1)作斜率为1的直线交圆C 2020-06-09 …
椭圆、抛物线以椭圆E:(x^2)/4+y^2=1的上顶点为焦点的抛物线C的标准方程为x^2=2py 2020-06-21 …
已知椭圆C的中心在原点,焦点在x轴上,它的一个顶点恰好是抛物线x2=4y的焦点,离心率等于255. 2020-07-19 …
以抛物线C的顶点为圆心的圆交C于A、B两点,交C的准线于D、E两点.已知|AB|=42,|DE|= 2020-07-22 …
已知椭圆C:x平方/a平方+y平方/b平方=1(a大于b大于0)的短轴长与焦距相等,且过定点(1, 2020-07-31 …