设椭圆C：x2a2+y2b2=1(a>b>0)的左右焦点分别为F1，F2，过点F1的直线与C交于点P，Q．若|PF2|=|F1F2|，且3|PF1|=4|QF1|，则ba的值为（）A.35B.57C.267D.265

Question

设椭圆C：

(x2)/(a2)+(y2)/(b2)=1(a>b>0)的左右焦点分别为F₁，F₂，过点F₁的直线与C交于点P，Q．若|PF₂|=|F₁F₂|，且3|PF₁|=4|QF₁|，则(b)/(a)的值为（　　）

A.

(3)/(5)

B.

(5)/(7)

C.

(2√(6))/(7)

D.

(2√(6))/(5)

Answer 1

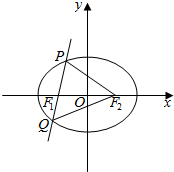如图所示，
∵|PF₂|=|F₁F₂|，
∴|PF₂|=2c，则|PF₁|=2a-2c．
∵3|PF₁|=4|QF₁|，
∴|QF₁|=(3)/(4)(2a-2c)=(3)/(2)(a-c)，
则|QF2|=2a-(3)/(2)(a-c)=(a)/(2)+(3)/(2)c．
在等腰△PF₁F₂中，可得cos∠PF₁F₂=((1)/(2)|PF1|)/(|F1F2|)=(a-c)/(2c)．
在△QF₁F₂中，由余弦定理可得：cos∠QF₁F₂=((9)/(4)(a-c)2+4c2-(1)/(4)(a+3c)2)/(2×2c×(3)/(2)(a-c))，
由cos∠PF₁F₂+cos∠QF₁F₂=0，得
(a-c)/(2c)+((9)/(4)(a-c)2+4c2-(1)/(4)(a+3c)2)/(2×2c×(3)/(2)(a-c))=0，
整理得：(5a-7c)/(6c)=0，∴5a=7c，
则25a²=49c²=49（a²-b²），
∴(b2)/(a2)=(24)/(49)，即(b)/(a)=(2√(6))/(7)．
故选：C．