在△ABC中，内角A，B，C所对的边分别是a，b，c，已知acosB=bcosA，边BC上的中线长为4，则△ABC面积的最大值是（）A.9B.283C.323D.12

Question

在△ABC中，内角A，B，C所对的边分别是a，b，c，已知acosB=bcosA，边BC上的中线长为4，则△ABC面积的最大值是（　　）

A. 9

B.

(28)/(3)

C.

(32)/(3)

D. 12

Answer 1

△ABC中，acosB=bcosA，
 由正弦定理得sinAcosB=sinBcosA，
∴sin（A-B）=0，
故A=B；
 由A=B知a=b，
又a²=b²+c²-2bccosA，
∴c=2acosA；
△ABD中，

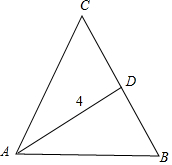
由余弦定理得4²=c²+((a)/(2))2-2c•(a)/(2)cosB，
∴a²=(64)/(1+8cos2A)；
∴△ABC的面积为
S=(1)/(2)acsinA
=(64sinAcosA)/(sinA2+9cos2A)
=(64tanA)/(tan2A+9)
=(64)/(tanA+(9)/(tanA))，
由基本不等式得
S≤(64)/(2×√(tanA•(9)/(tanA)))=(32)/(3)，
当且仅当tanA=3时，等号成立．
∴△ABC面积的最大值为(32)/(3)．
故选：C．