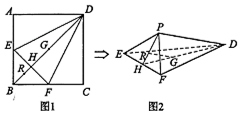
如图l，在正方形ABCD中，点E，F分别是AB，BC的中点，BD与EF交于点H，点G，R分别在线段DH，HB上，且DGGH=BRRH．将△AED，△CFD，△BEF分别沿DE，DF，EF折起，使点A，B，C重合于点P，如图2所示，（I）

Question

如图l，在正方形ABCD中，点E，F分别是AB，BC的中点，BD与EF交于点H，点G，R分别在线段DH，HB上，且(DG)/(GH)=(BR)/(RH)．将△AED，△CFD，△BEF分别沿DE，DF，EF折起，使点A，B，C重合于点P，如图2所示，
（I）求证：GR⊥平面PEF；
（Ⅱ）若正方形ABCD的边长为4，求三棱锥P-DEF的内切球的半径．

Answer 1

证明：（Ⅰ）在正方形ABCD中，∠A、∠B、∠C均为直角，
∴在三棱锥P-DEF中，PE，PF，PD三条线段两两垂直，
∴PD⊥平面PEF，
∵(DG)/(GH)=(BR)/(RH)，即(DG)/(GH)=(PR)/(RH)，∴在△PDH中，RG∥PD，
∴GR⊥平面PEF．
（Ⅱ）正方形ABCD边长为4，
由题意PE=PF=2，PD=4，EF=2√(2)，DF=2√(5)，
∴S_△PDF=2，S_△DEF=S_△DPE=4，
S△DEF=(1)/(2)×2√(2)×√((2√(5))2-(√(2))2)=6，
设三棱锥P-DEF的内切球半径为r，
则三棱锥的体积：
VP-DEF=(1)/(6)×2×2×4=(1)/(3)(S△PEF+2S△DPF+S△DEF)•r，
解得r=(1)/(2)，
∴三棱锥P-DEF的内切球的半径为(1)/(2)．