早教吧作业答案频道 -->数学-->
如图1,已知△ABC是等腰三角形,AB=AC,点D,E分别在AB,AC上,AD=AE.(1)发现探究:若将图1中的△ADE绕点A顺时针旋转α(0°<α<180°)到图2位置,则DB与CE有何数量关系,请给予证明.(2
题目详情
如图1,已知△ABC是等腰三角形,AB=AC,点D,E分别在AB,AC上,AD=AE.
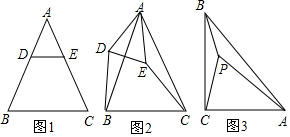
(1)发现探究:若将图1中的△ADE绕点A顺时针旋转α(0°<α<180°)到图2位置,则DB与CE有何数量关系,请给予证明.
(2)拓展运用:如图3,P是等腰直角三角形ABC内一点,∠ACB=90°,且PB=1,PC=2,PA=3,求∠BPC的度数.
(1)发现探究:若将图1中的△ADE绕点A顺时针旋转α(0°<α<180°)到图2位置,则DB与CE有何数量关系,请给予证明.
(2)拓展运用:如图3,P是等腰直角三角形ABC内一点,∠ACB=90°,且PB=1,PC=2,PA=3,求∠BPC的度数.

▼优质解答
答案和解析
(1)DB=CE.
理由:由旋转性质可知∠DAB=∠EAC,
在△DAB和△EAC中,
得
,
∴△DAB≌△EAC,
∴DB=CE;
(2)如图,将△CPB绕点C旋转90°得△CEA,连接PE,
∴△CPB≌△CEA,
∴CE=CP=2,AE=BP=1,∠PCE=90°,
∴∠CEP=∠CPE=45°,
在Rt△PCE中,由勾股定理可得,PE=2
,
在△PEA中,PE2=(2
)2=8,AE2=12=1,PA2=32=9,
∵PE2+AE2=AP2,
∴△PEA是直角三角形,
∴∠PEA=90°,
∴∠CEA=135°,
又∵△CPB≌△CEA,
∴∠BPC=∠CEA=135°.
理由:由旋转性质可知∠DAB=∠EAC,
在△DAB和△EAC中,
得
|
∴△DAB≌△EAC,
∴DB=CE;
(2)如图,将△CPB绕点C旋转90°得△CEA,连接PE,
∴△CPB≌△CEA,
∴CE=CP=2,AE=BP=1,∠PCE=90°,
∴∠CEP=∠CPE=45°,
在Rt△PCE中,由勾股定理可得,PE=2
| 2 |
在△PEA中,PE2=(2
| 2 |
∵PE2+AE2=AP2,
∴△PEA是直角三角形,
∴∠PEA=90°,
∴∠CEA=135°,
又∵△CPB≌△CEA,
∴∠BPC=∠CEA=135°.
看了 如图1,已知△ABC是等腰三...的网友还看了以下:
已知函数f(x)=ax,0<x≤1logax,x>1(a>0且a≠1),若f(3a2)>f(1-2 2020-05-13 …
1,一元二次方程ax²+bx+c=0(a≠0),求解公式为_________ 2,设A:(-1、1 2020-05-16 …
关于直线的解析几何已知点P(a,b)与Q(1,0)在直线2x-3y+1=0的两侧,则下列两种说法哪 2020-05-22 …
随机变量a服从正态分布N(1,σ2),且P(0<a<1)=0.3000.已知a>0,a≠1,则函数 2020-06-10 …
下列集合A到集合B的对应f是映射的是()A.A={-1,0,1},B={-1,0,1},f:A中的 2020-07-12 …
已知定义在R上的函数f(x)=log2(ax-b+1)(a>0,a≠1)的图象如图所示,则a,b满 2020-07-22 …
下列集合A到集合B的对应f不是函数的有()①A={-1,0,1},B={-1,0,1},f:A中的 2020-07-29 …
下列集合A到集合B的对应f是映射的是()A.A={-1,0,1},B={-1,0,1},f:A中的 2020-07-30 …
⒈已知分段函数f(x)=(a-1)x+5x≥0;﹣x²+ax+ax<0在(-∞,﹢∞)上为增函数, 2020-08-01 …
已知函数y=loga(x+c)(a,c为常数,其中a>0,a≠1)的图象如图所示,则下列结论成立的是 2020-11-01 …