早教吧作业答案频道 -->数学-->
已知等边△ABC,M是边BC延长线上一点,连接AM交△ABC的外接圆于点D,延长BD至N,使得BN=AM,连接CN,MN,解答下列问题:(1)猜想△CMN的形状,并证明你的结论;(2)请你证明CN是O的切线;
题目详情
已知等边△ABC,M是边BC延长线上一点,连接AM交△ABC的外接圆于点D,延长BD至N,使得BN=AM,连接CN,MN,解答下列问题:
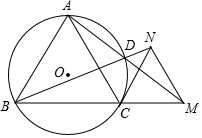
(1)猜想△CMN的形状,并证明你的结论;
(2)请你证明CN是 O的切线;
(3)若等边△ABC的边长是2,求AD•AM的值.

(1)猜想△CMN的形状,并证明你的结论;
(2)请你证明CN是 O的切线;
(3)若等边△ABC的边长是2,求AD•AM的值.
▼优质解答
答案和解析
 (1)△CMN是等边三角形,
(1)△CMN是等边三角形,
理由:在△BCN与△ACM中,
,
∴△BCN≌△ACM,
∴CN=CM,∠BCN=∠ACM,
∴∠BCN-∠ACN=∠ACM-∠ACN,
即∠MCN=∠ACB=60°,
∴△CMN是等边三角形;
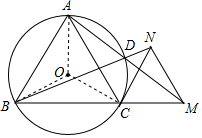
(2)连接OA.OB.OC,
在△BOC与△AOC中,
,
∴△BOC≌△AOC,
∴∠ACO=∠BCO=
∠ACB=30°,
∵∠ACB=∠MCN=60°,
∴∠ACN=60°,
∴∠OCN=90°,
∴OC⊥CN,
∴CN是 O的切线;
(3)∵∠ADB=∠ACB=60°,
∴∠ADB=∠ABC,
∵∠BAD=∠MAB,
∴△ABD∽△AMB,
∴
=
,
∴AD•AM=AB2=22=4.
 (1)△CMN是等边三角形,
(1)△CMN是等边三角形,理由:在△BCN与△ACM中,
|
∴△BCN≌△ACM,
∴CN=CM,∠BCN=∠ACM,
∴∠BCN-∠ACN=∠ACM-∠ACN,
即∠MCN=∠ACB=60°,
∴△CMN是等边三角形;
(2)连接OA.OB.OC,
在△BOC与△AOC中,
|
∴△BOC≌△AOC,
∴∠ACO=∠BCO=
| 1 |
| 2 |
∵∠ACB=∠MCN=60°,
∴∠ACN=60°,
∴∠OCN=90°,
∴OC⊥CN,
∴CN是 O的切线;
(3)∵∠ADB=∠ACB=60°,
∴∠ADB=∠ABC,
∵∠BAD=∠MAB,
∴△ABD∽△AMB,
∴
| AB |
| AM |
| AD |
| AB |
∴AD•AM=AB2=22=4.
看了 已知等边△ABC,M是边BC...的网友还看了以下:
广义表运算 head(tail(((a,b).(c,d))))答案是(c,d) 是怎么 出来 好难 2020-04-05 …
求半圆的周长时用公式:C=2πr÷2+2r或者是C=πd÷2+d. 2020-04-12 …
求半圆的周长时用公式:C=2πr÷2+2r或者是C=πd÷2+d. 2020-04-12 …
(答案是C,D) 请写出分析过程( HP22)a克 Mg、Al合金完全溶解在C1 mol·L-1、 2020-05-16 …
氯元素构成的双原子分子有三种,其相对分子质量分别为70.72.74,此三种分子个数比为6:3:1, 2020-05-16 …
设方程(x-a)(x-b)-x=0的两根是c,d设方程(x-a)(x-b)-x=0的两根是c,d, 2020-06-13 …
如图,在平面直角坐标系中,以点C(0,4)为圆心,半径为4的圆交y轴正半轴于点A,AB是⊙C的切线 2020-06-14 …
如图,已知多面体ABCD-A1B1C1D1,它是由一个长方体ABCD-A'B'C'D'切割而成,这 2020-06-27 …
如图,在△ABC中,AC=BC,AB是⊙C的切线,切点为D,直线AC交⊙C于点E、F,且CF=12 2020-07-09 …
三角形的∠CAD+∠B+∠C+∠D+∠E的读书是否变化从左到右分别是∠B,∠A,∠E,下面是∠C, 2020-07-16 …