早教吧作业答案频道 -->数学-->
如图,△ABC和△CDE是等腰直角三角形,∠BAC=∠CED=∠BCE=90°.点M为BC边上一点,连接EM、BD交于点N,点N恰好是BD中点,连接AN.(1)求证:MN=EN;(2)连接AM、AE,请探究AN与EN的位置关系与
题目详情
如图,△ABC和△CDE是等腰直角三角形,∠BAC=∠CED=∠BCE=90°.点M为BC边上一点,连接EM、BD交于点N,点N恰好是BD中点,连接AN.
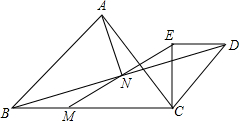
(1)求证:MN=EN;
(2)连接AM、AE,请探究AN与EN的位置关系与数量关系.
①写出AN与EM:位置关系___;数量关系___;
②请证明上述结论.

(1)求证:MN=EN;
(2)连接AM、AE,请探究AN与EN的位置关系与数量关系.
①写出AN与EM:位置关系___;数量关系___;
②请证明上述结论.
▼优质解答
答案和解析
(1)证明:∵∠CED=∠BCE=90°,
∴BC∥DE,
∴∠MBN=∠EDN,
∵点N恰好是BD中点,
∴BN=DN,
在△BMN和△DEN中,
,
∴△BMN≌△DEN(ASA),
∴MN=EN;
(2)①位置关系:AN⊥EM,数量关系:AN=
EM.
故答案为:AN⊥EM,AN=
EM.
②证明:连接AM,AE,
∵△BMN≌△DEN,
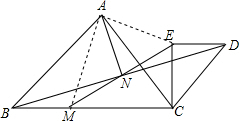 ∴BM=DE,
∴BM=DE,
∵△ABC和△CDE是等腰直角三角形,
∴AB=AC,∠ABM=∠ACB=45°,DE=CE,
∴BM=CE,
∵∠BCE=90°,
∴∠ACE=45°,
∴∠ABM=∠ACE,
在△ABM和△ACE中,
,
∴△ABM≌△ACE(SAS),
∴AM=AE,∠BAM=∠CAE,
∴∠BAM+∠CAM=∠CAE+∠CAM,
即∠MAE=∠BAC=90°,
∵MN=EN,
∴AN⊥EM,AN=
EM.
∴BC∥DE,
∴∠MBN=∠EDN,
∵点N恰好是BD中点,
∴BN=DN,
在△BMN和△DEN中,
|
∴△BMN≌△DEN(ASA),
∴MN=EN;
(2)①位置关系:AN⊥EM,数量关系:AN=
| 1 |
| 2 |
故答案为:AN⊥EM,AN=
| 1 |
| 2 |
②证明:连接AM,AE,
∵△BMN≌△DEN,
 ∴BM=DE,
∴BM=DE,∵△ABC和△CDE是等腰直角三角形,
∴AB=AC,∠ABM=∠ACB=45°,DE=CE,
∴BM=CE,
∵∠BCE=90°,
∴∠ACE=45°,
∴∠ABM=∠ACE,
在△ABM和△ACE中,
|
∴△ABM≌△ACE(SAS),
∴AM=AE,∠BAM=∠CAE,
∴∠BAM+∠CAM=∠CAE+∠CAM,
即∠MAE=∠BAC=90°,
∵MN=EN,
∴AN⊥EM,AN=
| 1 |
| 2 |
看了 如图,△ABC和△CDE是等...的网友还看了以下:
一道线性代数证明题:A为n阶实矩阵,其特征值全为实数,且AA'=A'A 证明:A=A' (A'是A 2020-04-05 …
已知:如图,在正方形ABCD外取一点E,连接AE、BE、DE.过点A作AE的垂线交DE于点P.若A 2020-05-16 …
△ABD△BCE都是等边三角形,且ABC三点共线,AE与BD交于M,AE与CD交于N,AE与CD交 2020-05-23 …
如图,过△ABC的顶点A作AE⊥BC,垂足为E.点D是射线AE上一动点(点D不与顶点A重合),连接 2020-06-27 …
Rt△ABC中,∠ABC=90°,在直线AB上取一点M,使AM=BC,过点A作AE⊥AB且AE=B 2020-07-22 …
有关转置矩阵,迷惑中.把一个m×n矩阵的行,列互换得到的n×m矩阵,称为A的转置矩阵,记为A'如何 2020-07-25 …
已知:如图,在正方形ABCD外取一点E,连接AE、BE、DE.过点A作AE的垂线交DE于点P.若A 2020-07-29 …
已知等腰Rt△ABC中,AB=AC,点A、C分别在y轴和x轴上.(1)如图1,若OA=2,求点B的 2020-08-01 …
线性代数1.已知A^2+2A+2I=0,I是n阶单位阵,则(A+I)^(-1)=?2线性代数1.已知 2020-11-02 …
线性代数:有道题——设a=(1,0,-1)T,矩阵A=aaT,n为正整数,求aE-A^n的行列式?请 2021-02-04 …