早教吧作业答案频道 -->数学-->
函数f(x)=4cos2x2cos(π2-x)-2sinx-|ln(x+1)|的零点个数为()A.1B.2C.3D.4
题目详情
函数f(x)=4cos2
cos(x 2
-x)-2sinx-|ln(x+1)|的零点个数为( )π 2
A. 1
B. 2
C. 3
D. 4
▼优质解答
答案和解析
 f(x)=4cos2
f(x)=4cos2
cos(
-x)-2sinx-|ln(x+1)|=4cos2
cos(
-x)-2sinx-|ln(x+1)|=sin2x-|ln(x+1)|
函数f(x)=4cos2
cos(
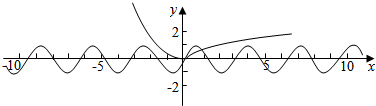
-x)-2sinx-|ln(x+1)|的零点个数为y=|ln(x+1)|与y=sin2x的图象的交点的个数,
作函数y=|ln(x+1)|与y=sin2x的图象,可得零点个数为2.
故选:B.
 f(x)=4cos2
f(x)=4cos2| x |
| 2 |
| π |
| 2 |
| x |
| 2 |
| π |
| 2 |
函数f(x)=4cos2
| x |
| 2 |
| π |
| 2 |
作函数y=|ln(x+1)|与y=sin2x的图象,可得零点个数为2.
故选:B.
看了 函数f(x)=4cos2x2...的网友还看了以下:
已知函数f(x)=x+根号2/x的定义域为(0,+),设点P是函数f(x)图象上的任意一点已知函数 2020-05-12 …
A,B,各多少角度?用常数m,n,x,y,z来表示,注意根号里面为x*x+y*y的和.忘记了计算公 2020-05-13 …
数字信号处理题:x(n)是一实序列,知道8点的DFT为X(k),知道X(0)X(1)X(2)X(3 2020-05-17 …
导数相关的题.1.当K取何值时,分段函数:x不等于0时,f(x)=x的k次方乘以sin(1/x), 2020-06-11 …
如图,直线AB的函数解析式为y=x+2分别与x、y轴交于点A,点B,直线CD的函数解析为y=2x- 2020-06-14 …
如图,已知直线OA的解析式为y=x,直线AC垂直x轴于点C,点C的坐标为(2,0),直线OA关于直 2020-06-14 …
如图,已知AF=2,点A,B分别是某函数图象与x轴,y轴的交点,点P是此图象上的一动点,设点P的横 2020-06-14 …
列方程计算.三个连续整数的积是120.1.若这三个数中,中间的一个数为X,则比它小1的数是,比它大 2020-06-27 …
如图,在平面直角坐标系中,点A为双曲线y=k/x(x>0)上一点(要有过程)如图,在平面直角坐标系 2020-07-08 …
求函数的驻点f'x(x,y)=2xy(4-x-y)-x^2y=0.(1)其中f'x(x,y)中左边 2020-07-11 …