早教吧作业答案频道 -->数学-->
二次函数y═ax2+bx+c的图象如图所示,下列结论:①b<2a;②a+2c-b>0;③b>a>c;④b2+2ac<3ab.其中正确结论的个数是.
题目详情
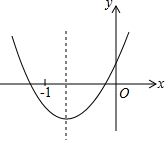
二次函数y═ax2+bx+c的图象如图所示,下列结论:①b<2a;②a+2c-b>0;③b>a>c;④b2+2ac<3ab.其中正确结论的个数是___.

▼优质解答
答案和解析
由图象可知,a>0,b>0,c>0,
∵-
>-1,
∴b<2a,故①正确,
假如|a-b+c|<c,
则∵a-b+c<0,
∴-a+b-c>0,
∵c>0,
∴-a+b-c<c,
∴a-b+2c>0,则②正确,
由于无法判定|a-b+c|与c的大小,故②错误.
∵-
<-
,
∴b>a,
∵x1<-1,x2>-
,
∴x1•x2<1,
∴
<1,
∴a>c,
∴b>a>c,故③正确,
∵b2-4ac>0,
∴2ac<
b2,
∵b<2a,
∴
b2<3ab,
∴
b2=b2+
b2>b2+2ac,
b2+2ac<
b2<3ab,
∴b2+2ac<3ab.故④正确.
故①③④.
∵-
| b |
| 2a |
∴b<2a,故①正确,
假如|a-b+c|<c,
则∵a-b+c<0,
∴-a+b-c>0,
∵c>0,
∴-a+b-c<c,
∴a-b+2c>0,则②正确,
由于无法判定|a-b+c|与c的大小,故②错误.
∵-
| b |
| 2a |
| 1 |
| 2 |
∴b>a,
∵x1<-1,x2>-
| 1 |
| 2 |
∴x1•x2<1,
∴
| c |
| a |
∴a>c,
∴b>a>c,故③正确,
∵b2-4ac>0,
∴2ac<
| 1 |
| 2 |
∵b<2a,
∴
| 3 |
| 2 |
∴
| 3 |
| 2 |
| 1 |
| 2 |
b2+2ac<
| 3 |
| 2 |
∴b2+2ac<3ab.故④正确.
故①③④.
看了 二次函数y═ax2+bx+c...的网友还看了以下:
已知函数f(x)=(根号3sinωx/2+cosωx/2)cosωx/2-1/2,(ω>0)的最小 2020-04-12 …
关于三角函数的数学题目,在△ABC中,内角A,B,C所对的边长分别为a,b,c,已知c=2,C=6 2020-04-26 …
数学三角函数题急在三角形ABC中,角A,B,C所对的边是a,b,c.已知(a+b):(b+c):( 2020-04-26 …
帮忙解个三角函数吖在三角形ABC中,A.B为锐角,角A.B.C所对的边分别为,a.b.c且sinA 2020-05-13 …
速度……在△ABC中,∠A,∠B,∠C所对的边分别为a,b,c,且a,b,c依次成等差在△ABC中 2020-06-15 …
已知三角形abc的内角A,B,C所对的边分别为a,b,c,已知b^2+c^2-a^2=bc(1)求 2020-07-22 …
在△ABC中,角A,B,C所对的边分别为a,b,c,函数f(x)=2cosxsin(x-A)+si 2020-07-30 …
已知函数f(x)=4cosxsin(x-π/3)-√3已知函数f(x)=4cosxsin(x-π/3 2020-11-01 …
在△ABC中,三内角A,B,C所对的边分别为a,b,c,若B=60°,c=(根号3-1)a1.求角C 2020-11-02 …
三角函数已知函数f(x)=cos(2x-π/3)+2sin(x–π/4)sin(x+π/4)(1). 2020-12-08 …